题目内容
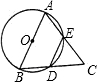 如图所示,AB是⊙O的直径,AB=AC,D,E在⊙O上,说明BD=DE.
如图所示,AB是⊙O的直径,AB=AC,D,E在⊙O上,说明BD=DE.
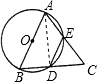 证明:连接AD,
证明:连接AD,∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC.
又AB=AC,
∴∠BAD=∠EAD,
∴
 ,
,∴BD=DE.
分析:证BD=DE,可证两弦所对的劣弧相等.连接AD;由AB是⊙O的直径得到AD⊥BC;
由等腰三角形三线合一的性质,可得出AD平分∠BAC,即弧BD=弧DE,由此得证.
点评:本题主要考查了等腰三角形的性质,以及圆周角定理的应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
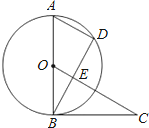 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.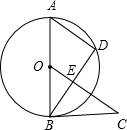 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.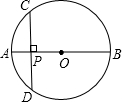 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为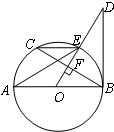 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. 如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )
如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )