题目内容
在如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )

A.8 B.2 C.2
C.2 D.2+2
D.2+2
C.
【解析】
试题分析:把此正方体的DCC1D1面与CC1B1B面展开在同一平面内,然后利用勾股定理求点M和N点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形MNB1中,一条直角边长等于6,另一条直角边长等于2,利用勾股定理可求得.
试题解析:把正方体的DCC1D1面与CC1B1B面展开在同一平面内,
∵M、N为C1D1和BB1的中点,
∴NB1=2,MC1=2,
在Rt△NMB1中,MN=
故选C.
考点:平面展开-最短路径问题.
考点分析: 考点1:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 考点2:立体图形 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 的方程
的方程 是一元二次方程,则
是一元二次方程,则 .
. 的对称轴是:( )
的对称轴是:( ) B.直线
B.直线 C.y轴 D.x轴
C.y轴 D.x轴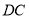 ,DC2=DE·DA是否成立?若成立,给出证明;若不成立,举例说明.
,DC2=DE·DA是否成立?若成立,给出证明;若不成立,举例说明.
 BC),当 或 或 时,△ADE与△ABC相似。
BC),当 或 或 时,△ADE与△ABC相似。





