题目内容
已知当 时,二次函数y=ax2+bx+c取得最值
时,二次函数y=ax2+bx+c取得最值 ,且函数图象过点A(0,1).
,且函数图象过点A(0,1).
(1)求a,b,c的值;
(2)把函数y=ax2+bx+c图象向左平移d个单位后所得函数图象的解析式是y=ax2+x+e,试求e的值;
(3)若函数y=ax2+x+e的图象与x轴交于两点A(α,0),B(β,0),且A点在B点左边,试求2α4-α3+α2+3α-5的值.
解:(1)∵当x= 时,二次函数y=ax2+bx+c取得最值
时,二次函数y=ax2+bx+c取得最值 ,
,
∴y=ax2+bx+c=a(x- )2-
)2- ,
,
∵图象过点A(0,1)得: a-
a- =1.
=1.
∴a=1.
∴y=(x- )2-
)2- =x2-3x+1,
=x2-3x+1,
∴a=1,b=-3,c=1.
(2)平移后,函数图象的顶点是( -d,-
-d,- ).
).
函数式为:y=(x- +d)2-
+d)2- =x2+(2d-3)x+d2-3d+1,
=x2+(2d-3)x+d2-3d+1,
∵函数图象的解析式是y=ax2+x+e,
∴2d-3=1,e=d2-3d+1.
解得d=2,e=-1.
(3)∴y=ax2+x+e=x2+x-1,
∵函数y=ax2+x+e的图象与x轴交于两点A(α,0),B(β,0),且A点在B点左边,
∴α是方程x2+x-1=0的较小根.
∴α2=1-α,且α=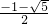 .
.
∴2α4-α3+α2+3α-5=2(1-α)2-α(1-α)+1-α+3α-5
=3a2-3a-2=1-6a=4+3 .
.
分析:(1)由当 时,二次函数y=ax2+bx+c取得最值
时,二次函数y=ax2+bx+c取得最值 ,即可得y=ax2+bx+c=a(x-
,即可得y=ax2+bx+c=a(x- )2-
)2- ,又由函数图象过点A(0,1),利用待定系数法即可求得此二次函数的解析式,即可求得a,b,c的值;
,又由函数图象过点A(0,1),利用待定系数法即可求得此二次函数的解析式,即可求得a,b,c的值;
(2)由函数y=ax2+bx+c图象向左平移d个单位后所得函数图象的解析式是y=ax2+x+e,即可知平移后,函数图象的顶点是( -d,-
-d,- ),然后可得顶点式,再整理成一般式,根据多项式相等的知识,即可求得e的值;
),然后可得顶点式,再整理成一般式,根据多项式相等的知识,即可求得e的值;
(3)由函数y=ax2+x+e的图象与x轴交于两点A(α,0),B(β,0),且A点在B点左边,即可得α是方程x2+x-1=0的较小根,继而求得:α2=1-α与α的值,然后化简2α4-α3+α2+3α-5,再代入α的值即可求得答案.
点评:此题考查了二次函数的顶点式与一般式的转化,点与函数的关系,待定系数法求函数的解析式等知识.此题综合性较强,难度较大,解题的关键是方程思想与整体思想的应用.
 时,二次函数y=ax2+bx+c取得最值
时,二次函数y=ax2+bx+c取得最值 ,
,∴y=ax2+bx+c=a(x-
 )2-
)2- ,
,∵图象过点A(0,1)得:
 a-
a- =1.
=1.∴a=1.
∴y=(x-
 )2-
)2- =x2-3x+1,
=x2-3x+1,∴a=1,b=-3,c=1.
(2)平移后,函数图象的顶点是(
 -d,-
-d,- ).
).函数式为:y=(x-
 +d)2-
+d)2- =x2+(2d-3)x+d2-3d+1,
=x2+(2d-3)x+d2-3d+1,∵函数图象的解析式是y=ax2+x+e,
∴2d-3=1,e=d2-3d+1.
解得d=2,e=-1.
(3)∴y=ax2+x+e=x2+x-1,
∵函数y=ax2+x+e的图象与x轴交于两点A(α,0),B(β,0),且A点在B点左边,
∴α是方程x2+x-1=0的较小根.
∴α2=1-α,且α=
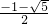 .
.∴2α4-α3+α2+3α-5=2(1-α)2-α(1-α)+1-α+3α-5
=3a2-3a-2=1-6a=4+3
 .
.分析:(1)由当
 时,二次函数y=ax2+bx+c取得最值
时,二次函数y=ax2+bx+c取得最值 ,即可得y=ax2+bx+c=a(x-
,即可得y=ax2+bx+c=a(x- )2-
)2- ,又由函数图象过点A(0,1),利用待定系数法即可求得此二次函数的解析式,即可求得a,b,c的值;
,又由函数图象过点A(0,1),利用待定系数法即可求得此二次函数的解析式,即可求得a,b,c的值;(2)由函数y=ax2+bx+c图象向左平移d个单位后所得函数图象的解析式是y=ax2+x+e,即可知平移后,函数图象的顶点是(
 -d,-
-d,- ),然后可得顶点式,再整理成一般式,根据多项式相等的知识,即可求得e的值;
),然后可得顶点式,再整理成一般式,根据多项式相等的知识,即可求得e的值;(3)由函数y=ax2+x+e的图象与x轴交于两点A(α,0),B(β,0),且A点在B点左边,即可得α是方程x2+x-1=0的较小根,继而求得:α2=1-α与α的值,然后化简2α4-α3+α2+3α-5,再代入α的值即可求得答案.
点评:此题考查了二次函数的顶点式与一般式的转化,点与函数的关系,待定系数法求函数的解析式等知识.此题综合性较强,难度较大,解题的关键是方程思想与整体思想的应用.

练习册系列答案
相关题目
已知:二次函数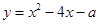 ,下列说法中错误的是( )
,下列说法中错误的是( )
A.当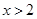 时, 时,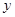 随 随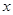 的增大而增大 的增大而增大 |
B.若图象与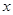 轴有交点,则 轴有交点,则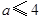 |
C.当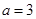 时,二次函数 时,二次函数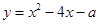 有最小值为-7 有最小值为-7 |
D.若将图象向上平移1个单位,再向左平移3个单位后过点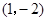 ,则 ,则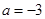 |
 时,二次函数y=ax2+bx+c取得最值
时,二次函数y=ax2+bx+c取得最值 ,且函数图象过点A(0,1).
,且函数图象过点A(0,1). .
. 时,二次函数的图像与
时,二次函数的图像与 轴有两个不同交点;
轴有两个不同交点; ,
, ,顶点为
,顶点为 ,且△
,且△ 的面积为
的面积为 ,求此二次函数的函数表达式.
,求此二次函数的函数表达式. ,下列说法中错误的是( )
,下列说法中错误的是( ) 时,
时, 随
随 的增大而增大 B.若图象与
的增大而增大 B.若图象与
 时,二次函数
时,二次函数 ,则
,则