题目内容
（2013•长春）如图，△ABC内接于⊙O，∠ABC=71°，∠CAB=53°，点D在AC弧上，则∠ADB的大小为（ ）分析：根据三角形内角和定理求出∠ACB，根据圆周角定理得出∠C，求出即可．
解答：解：∵∠ABC=71°，∠CAB=53°，
∴∠ACB=180°-∠ABC-∠BAC=56°，
∵弧AB对的圆周角是∠ADB和∠ACB，
∴∠ADB=∠ACB=56°，
故选C．
∴∠ACB=180°-∠ABC-∠BAC=56°，
∵弧AB对的圆周角是∠ADB和∠ACB，
∴∠ADB=∠ACB=56°，
故选C．
点评：本题考查了圆周角定理和三角形内角和定理的应用，关键是求出∠ACB的度数和得出∠ACB=∠ADB．
练习册系列答案
阅读快车系列答案
相关题目
（2013•长春）如图是由四个相同的小长方体组成的立体图形，这个立体图形的正视图是（ ）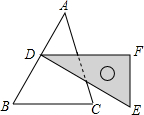
（2013•长春）如图，含30°角的直角三角尺DEF放置在△ABC上，30°角的顶点D在边AB上，DE⊥AB．若∠B为锐角，BC∥DF，则∠B的大小为（ ）
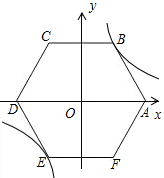（2013•长春）如图，在平面直角坐标系中，边长为6的正六边形ABCDEF的对称中心与原点O重合，点A在x轴上，点B在反比例函数