题目内容
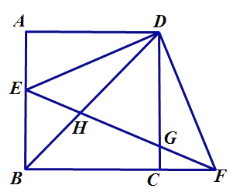
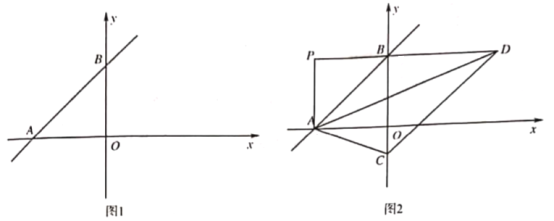
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() ,
,![]() 重合).以
重合).以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
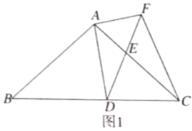
(1)求证:![]() ;
;
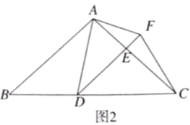
(2)当![]() 时(如图2),求
时(如图2),求![]() 的长;
的长;
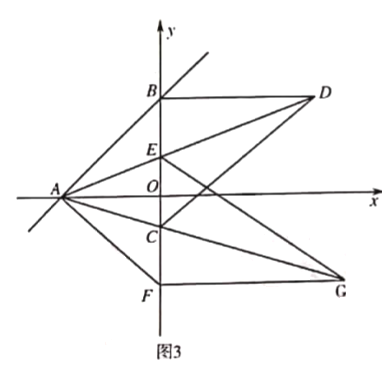
(3)点![]() 在
在![]() 边上运动的过程中,是否存在某个位置,使得
边上运动的过程中,是否存在某个位置,使得![]() ?若存在,求出此时
?若存在,求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)详见解析;(2)![]() ;(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF,此时BD=9.
;(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF,此时BD=9.
【解析】
(1)利用等腰三角形的性质有∠B=∠ACB,然后根据∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B即可得出∠BAD=∠CDE,则结论可证;
(2)过点A作AM⊥BC于M,设![]() ,在
,在![]() 中利用勾股定理求出k的值,然后利用等腰三角形三线合一求出BC的长度,然后证明△ABD∽△CBA,
中利用勾股定理求出k的值,然后利用等腰三角形三线合一求出BC的长度,然后证明△ABD∽△CBA,
则![]() ,由此可求出DB的长度,最后再利用平行线分线段成比例有
,由此可求出DB的长度,最后再利用平行线分线段成比例有![]() ,即可求出AE的长度;
,即可求出AE的长度;
(3)作FH⊥BC于H,AM⊥BC于M,AN⊥FH于N,首先证明四边形AMHN为矩形,
则有∠MAN=90°,MH=AN,然后设![]() ,在
,在![]() 中利用勾股定理求出k的值,然后利用等腰三角形三线合一求出BC的长度,然后证明△AFN∽△ADM,
中利用勾股定理求出k的值,然后利用等腰三角形三线合一求出BC的长度,然后证明△AFN∽△ADM,
利用相似三角形的性质可求出AN的长度,进而求出CH的长度,再根据等腰三角形三线合一求出CD的长度,最后利用BD=BC-CD即可得出答案.
(1)证明:∵AB=AC,
∴∠B=∠ACB,
∵∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠CDE,
∴△BAD∽△DCE.
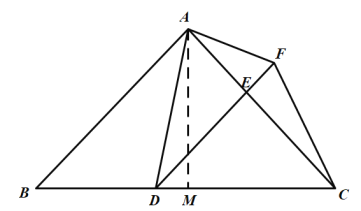
(2)解:过点A作AM⊥BC于M.
∵![]() ,
,
∴设![]() ,
,
![]()
∴![]()
解得![]() 或
或![]() (舍去)
(舍去)
∵AB=AC,AM⊥BC,
∴BC=2BM=2×4k=16,
∵DE∥AB,
∴∠BAD=∠ADE,
∵∠ADE=∠B,∠B=∠ACB,
∴∠BAD=∠ACB,
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴![]() ,
,
∴![]()
![]() ,
,
∵DE∥AB,
∴![]() ,
,
∴![]()
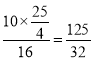 .
.
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.
理由:作FH⊥BC于H,AM⊥BC于M,AN⊥FH于N.
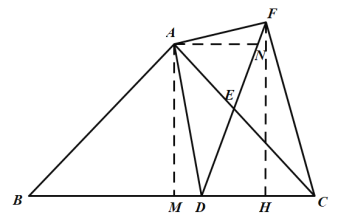
∵FH⊥BC,AM⊥BC,AN⊥FH,
∴∠NHM=∠AMH=∠ANH=90°,
∴四边形AMHN为矩形,
∴∠MAN=90°,MH=AN,
∵AN⊥FH,AM⊥BC,
∴∠ANF=90°=∠AMD,
∵∠DAF=90°=∠MAN,
∴∠NAF=∠MAD,
∴△AFN∽△ADM,
∴![]() ,
,
∴![]() ,
,
∴CH=CM-MH=CM-AN=8-![]() =
=![]() ,
,
当DF=CF时,由点D不与点C重合,可知△DFC为等腰三角形,
∵FH⊥DC,
∴CD=2CH=7,
∴BD=BC-CD=16-7=9,
∴点D在BC边上运动的过程中,存在某个位置,使得DF=CF,此时BD=9.

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案