题目内容
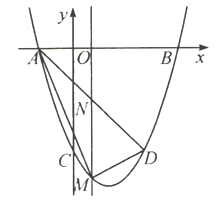
【题目】如图,抛物线y=(x1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,3),点D与C关于抛物线的对称轴对称.
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线上的一点,当△ABP的面积是8,求出点P的坐标;
(3)过直线AD下方的抛物线上一点M作y轴的平行线,与直线AD交于点N,已知M点的横坐标是m,试用含m的式子表示MN的长及△ADM的面积S,并求当MN的长最大时s的值.
【答案】(1)抛物线的解析式为y=(x1)2-4,点D的坐标为(2,-3);(2)P点的坐标为(1+2![]() ,4)或(1-2
,4)或(1-2![]() ,4)或(1,-4);(3)MN=
,4)或(1,-4);(3)MN=![]() (-1<m<2);S=
(-1<m<2);S=![]() (-1<m<2),当MN最长为
(-1<m<2),当MN最长为![]() 时,S的值为
时,S的值为![]() .
.
【解析】
(1)把C(0,3)代入y=(x1)2+n即可求解出n,得到抛物线解析式,再根据对称轴得到点D的坐标;
(2)令y=0,解出A,B的坐标,得到AB的长,设P(x,y),根据△ABP的面积是8求出y的值,再代入解析式即可求出P点坐标;
(3)根据A、D坐标求出直线AD的解析式,根据MN∥y轴,可设M[m, (m1)2-4],N(m,-m-1),根据MN=![]() (-1<m<2),再根据二次函数最值即可求出MN的最大值,再求出此时的S.
(-1<m<2),再根据二次函数最值即可求出MN的最大值,再求出此时的S.
(1)C(0,3)代入y=(x1)2+n
即-3=(01)2+n
解得n=-4,
∴抛物线的解析式为y=(x1)2-4,
∴抛物线的对称轴为x=1,
∵点D与C关于抛物线的对称轴对称.
∴点D的坐标为(2,-3);
(2)由y=(x1)2-4=0解得x1=-1,x2=3,
∵A在B的左侧
∴A(-1,0),B(3,0)
∴AB=AO+BO=4,
设P(x,y),
∵S△ABP=![]() =8
=8
∴![]() =8
=8
∴y=±4,
当(x1)2-4=4时,x1=1+2![]() ,x2=1-2
,x2=1-2![]() ,
,
∴P(1+2![]() ,4)或(1-2
,4)或(1-2![]() ,4)
,4)
当(x1)2-4=-4时,x1=x2=1,
∴P(1,-4)
综上,P点的坐标为(1+2![]() ,4)或(1-2
,4)或(1-2![]() ,4)或(1,-4);
,4)或(1,-4);
(3)设AD的直线为y=kx+b,
把A(-1,0)、D(2,-3)代入得![]()
解得![]()
∴y=-x-1
∵MN∥y轴,且点M的横坐标为m,
∴M[m, (m1)2-4],N(m,-m-1),
∴MN=![]() (-1<m<2)
(-1<m<2)
化简得MN=![]() (-1<m<2)
(-1<m<2)
当m=-![]() =
=![]() 时,MN最大,最大值为
时,MN最大,最大值为 =
=![]() ,
,
S△ADM= S△AMN+S△DMN=![]() =
=![]() (
(![]() )=
)=![]()
当m=![]() 时,S△ADM=
时,S△ADM=![]() =
=![]()
故MN=![]() (-1<m<2);
(-1<m<2);
S=![]() (-1<m<2),
(-1<m<2),
当MN最长时,S的值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 以2
以2![]() 的速度向点终点
的速度向点终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 以1
以1![]() 的速度向点终点
的速度向点终点![]() 运动,它们到达终点后停止运动.
运动,它们到达终点后停止运动.
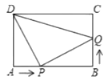
(1)几秒后,点![]() 、
、![]() 的距离是点
的距离是点![]() 、
、![]() 的距离的2倍;
的距离的2倍;
(2)几秒后,![]() 的面积是24
的面积是24![]() .
.
【题目】某课外学习小组根据学习函数的经验,对函数![]() 的图象与性质进行了探究请补充完整以下探索过程:
的图象与性质进行了探究请补充完整以下探索过程:
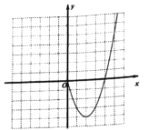
(1)列表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接写出![]() ________,
________,![]() ________;
________;
(2)根据上表中的数据,在平面直角坐标系内补全该函数的图象,并结合图象写出该函数的两条性质:
性质1______________________________________________________
性质2_______________________________________________________
(3)若方程![]() 有四个不同的实数根,请根据函数图象,直接写出k的取值范围.
有四个不同的实数根,请根据函数图象,直接写出k的取值范围.