题目内容
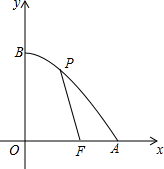 如图,已知点F的坐标为(3,0),点A,B分别是以y轴为对称轴的某二次函数部分图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是以y轴为对称轴的某二次函数部分图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-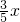 (0≤x≤5),则此二次函数的解析式为________.
(0≤x≤5),则此二次函数的解析式为________.
y2=- x2+16
x2+16
分析:过点P作PC⊥x轴于点C,根据勾股定理得PF2=PC2+FC2,建立关于x、y的函数关系式,从而得到关于x的二次函数.
解答: 解:过点P作PC⊥x轴于点C,
解:过点P作PC⊥x轴于点C,
则由勾股定理得:
PF2=PC2+FC2,
则d2=(3-x)2+y2,
∵d=5- x,
x,
∴(5- x)2=(3-x)2+y2.
x)2=(3-x)2+y2.
整理得,y2=- x2+16.
x2+16.
故答案为y2=- x2+16.
x2+16.
点评:本题考查了待定系数法求二次函数解析式、勾股定理,巧用P的坐标是解题的关键.
 x2+16
x2+16分析:过点P作PC⊥x轴于点C,根据勾股定理得PF2=PC2+FC2,建立关于x、y的函数关系式,从而得到关于x的二次函数.
解答:
 解:过点P作PC⊥x轴于点C,
解:过点P作PC⊥x轴于点C,则由勾股定理得:
PF2=PC2+FC2,
则d2=(3-x)2+y2,
∵d=5-
 x,
x,∴(5-
 x)2=(3-x)2+y2.
x)2=(3-x)2+y2.整理得,y2=-
 x2+16.
x2+16.故答案为y2=-
 x2+16.
x2+16.点评:本题考查了待定系数法求二次函数解析式、勾股定理,巧用P的坐标是解题的关键.

练习册系列答案
相关题目
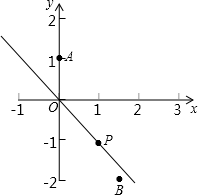 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(| 3 |
| 2 |
| A、(2,-2) | ||||
| B、(4,-4) | ||||
C、(
| ||||
| D、(5,-5) |
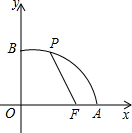 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-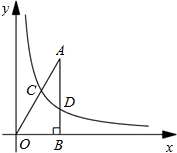 如图,已知点A的坐标为(
如图,已知点A的坐标为(

 如图,已知点A的坐标为(
如图,已知点A的坐标为(