题目内容
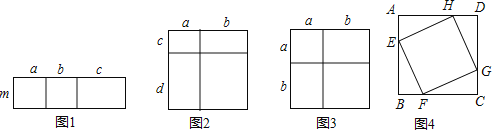
【题目】如图，分别连接正方形对边的中点，能将正方形划分成四个面积相等的小正方形用上述方法对一个边长为1的正方形进行划分，第1次划分得到图1，第2次划分图2，则第3次划分得到的图中共有______个正方形，借助划分得到的图形，计算
的结果为______（用含
的式子表示）
【答案】4n+1 
【解析】
（1）由第一次可得5个正方形，第二次可得9个正方形，第三次可得13个正方形，可得规律：第n次可得（4n+1）个正方形；
（2）此题可看作上面几何体面积问题，即可求得答案．
解：
(1)∵第一次可得5个正方形，第二次可得9个正方形，第三次可得13个正方形，
∴第n次可得(4n+1)个正方形，
(2)根据题意得：
原式=
=；
故答案为：（1）4n+1；（2）；
练习册系列答案
相关题目
