题目内容
20.(1)解方程:$\frac{1}{1-{x}^{2}}$=$\frac{3}{1-x}$-$\frac{5}{1+x}$(2)化简:$\frac{2x}{x+1}$-$\frac{2x+4}{{x}^{2}-1}$÷$\frac{x+2}{{x}^{2}-2x+1}$,然后在不等式x≤2的非负整数解中选择一个适当的数代入求值.
分析 (1)先把分式方程转化成整式方程,求出方程的解,最后进行检验即可;
(2)先分解因式,把除法变成乘法,算乘法,算减法,最后选择适当的数代入求出即可.
解答 解:(1)方程两边都乘以(1+x)(1-x)得:1=3(1+x)-5(1-x),
解得:x=$\frac{3}{8}$,
检验:∵当x=$\frac{3}{8}$时,(1+x)(1-x)≠0,
∴x=$\frac{3}{8}$是原方程的解,
∴原方程的解为x=$\frac{3}{8}$;
(2)原式=$\frac{2x}{x+1}$-$\frac{2(x+2)}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+2}$
=$\frac{2x}{x+1}$-$\frac{2(x-1)}{x+1}$
=$\frac{2}{x+1}$,
∵不等式x≤2的非负整数解为0,1,2,
又∵x≠±1,x≠-2,
∴把x=0代入得:原式=2.
点评 本题考查了解分式方程和分式的混合式运算和求值,能把分式方程转化成整式方程是解(1)的关键,能正确根据分式的运算法则进行化简是解(2)的关键,注意:解分式方程一定要进行检验.

练习册系列答案
相关题目
9.正方形具有而矩形不一定具有的性质是( )
| A. | 四个角都为直角 | B. | 对角线互相平分 | C. | 对角线相等 | D. | 对角线互相垂直 |
 如图,在数轴上点A和点B之间的整数是-1、0、1、2.
如图,在数轴上点A和点B之间的整数是-1、0、1、2.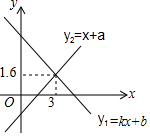 一次函数y1=kx+b与y2=x+a的图象如图所示,则关于x、y的方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=x+a}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=3}\\{y=1.6}\end{array}\right.$.
一次函数y1=kx+b与y2=x+a的图象如图所示,则关于x、y的方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=x+a}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=3}\\{y=1.6}\end{array}\right.$.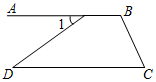 如图,若∠1=∠D=39°,∠C=51°,则∠B=129°.
如图,若∠1=∠D=39°,∠C=51°,则∠B=129°.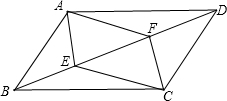 如图,在四边形ABCD中,AB∥CD,AD∥BC,现在请你添加一个适当的条件:BE=DF,使得四边形AECF为平行四边形(图中不再添加点和线).
如图,在四边形ABCD中,AB∥CD,AD∥BC,现在请你添加一个适当的条件:BE=DF,使得四边形AECF为平行四边形(图中不再添加点和线).


