题目内容
一次函数y=kx+b的图象与x轴和y轴的正半轴分别交于A,B两点.已知OA+OB=6(O为坐标原点).且S△ABO=4,则这个一次函数的解析式为
- A.
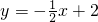
- B.y=-2x+4
- C.

- D.
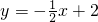 或y=-2x+4
或y=-2x+4
D
分析:首先根据题意设A(x,0),B(0,y),再根据“OA+OB=6(O为坐标原点).且S△ABO=4,”可得方程组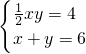 ,再解出x、y的值,进而得到A、B两点坐标.然后再利用待定系数法求出一次函数解析式.
,再解出x、y的值,进而得到A、B两点坐标.然后再利用待定系数法求出一次函数解析式.
解答:∵一次函数y=kx+b的图象与x轴和y轴的正半轴分别交于A,B两点.
∴设A(x,0),B(0,y),
∵OA+OB=6(O为坐标原点).且S△ABO=4,
∴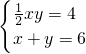 ,
,
解得: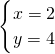 或
或 ,
,
∴A(2,0)、B(0,4)或A(4,0)、B(0,2),
当A(2,0)、B(0,4)时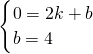 ,解得
,解得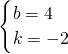 ,
,
当A(4,0)、B(0,2)时, ,解得
,解得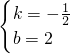 ,
,
∴这个一次函数的解析式为y=- x+2或y=-2x+4,
x+2或y=-2x+4,
故选:D.
点评:此题主要考查了待定系数法求一次函数解析式,关键是根据题意计算出一次函数图象所经过的点的坐标.
分析:首先根据题意设A(x,0),B(0,y),再根据“OA+OB=6(O为坐标原点).且S△ABO=4,”可得方程组
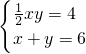 ,再解出x、y的值,进而得到A、B两点坐标.然后再利用待定系数法求出一次函数解析式.
,再解出x、y的值,进而得到A、B两点坐标.然后再利用待定系数法求出一次函数解析式.解答:∵一次函数y=kx+b的图象与x轴和y轴的正半轴分别交于A,B两点.
∴设A(x,0),B(0,y),
∵OA+OB=6(O为坐标原点).且S△ABO=4,
∴
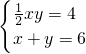 ,
,解得:
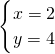 或
或 ,
,∴A(2,0)、B(0,4)或A(4,0)、B(0,2),
当A(2,0)、B(0,4)时
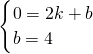 ,解得
,解得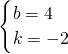 ,
,当A(4,0)、B(0,2)时,
 ,解得
,解得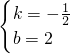 ,
,∴这个一次函数的解析式为y=-
 x+2或y=-2x+4,
x+2或y=-2x+4,故选:D.
点评:此题主要考查了待定系数法求一次函数解析式,关键是根据题意计算出一次函数图象所经过的点的坐标.

练习册系列答案
相关题目
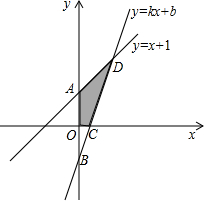 x轴以及y=x+1的图象分别交于点C、D.
x轴以及y=x+1的图象分别交于点C、D.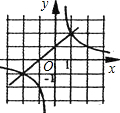 一次函数y=kx+b与反比例函数y=
一次函数y=kx+b与反比例函数y= (2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,
(2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,