题目内容
问题:如图1,在正方形ABCD内有一点P,PA=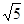 ,PB=
,PB=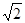 ,PC=1,求∠BPC的角度.
,PC=1,求∠BPC的角度.
分析:根据已知条件比较分散的特点,我们可以通过旋转变换,将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转900,得到了△BP1A(如图2),然后连接PP1.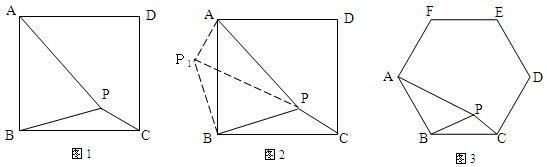
解决问题:请你通过计算求出图2中∠BPC的角度;
类比研究:如图3,若在正六边形ABCDEF内有一点P,且PA=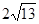 ,PB=4,PC=2.
,PB=4,PC=2.
(1)请你通过计算求出∠BPC的度数;
(2)直接写出正六边形ABCDEF的边长为 .
解决问题1350;类比研究(1)1200;(2)2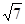
解析试题分析:(1)根据旋转的性质得到∠P′BP=90°,BP′=BP=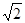 ,P′A=PC=1,∠BP′A=∠BPC,则△BPP′为等腰直角三角形,根据等腰直角三角形的性质得PP′=
,P′A=PC=1,∠BP′A=∠BPC,则△BPP′为等腰直角三角形,根据等腰直角三角形的性质得PP′=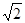 PB=2,∠BP′P=45°,利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,则∠BPC=∠BP′A=45°+90°=135°;
PB=2,∠BP′P=45°,利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,则∠BPC=∠BP′A=45°+90°=135°;
(2)把△BPC绕点B逆时针旋转120°,得到了△BP′A,根据旋转的性质得到∠P′BP=120°,BP′=BP=4,P′A=PC=2,∠BP′A=∠BPC,则∠BP′P=∠BPP′=30°,得到P′H=PH,利用含30°的直角三角形三边的关系得到BH=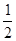 BP′=2,P′H=
BP′=2,P′H= BH=2
BH=2 ,得到P′P=2P′H=4
,得到P′P=2P′H=4 ,再利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,于是有∠BPC=∠BP′A=30°+90°=120°;过A作AG⊥BP′于G点,利用含30°的直角三角形三边的关系得到GP′=
,再利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,于是有∠BPC=∠BP′A=30°+90°=120°;过A作AG⊥BP′于G点,利用含30°的直角三角形三边的关系得到GP′=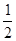 AP′=1,AG=
AP′=1,AG= GP′=
GP′= ,然后在Rt△AGB中利用勾股定理即可计算出AB长.
,然后在Rt△AGB中利用勾股定理即可计算出AB长.
(1)∵△BPC绕点B逆时针旋转90°,得到了△BP′A,
∴∠P′BP=90°,BP′=BP=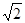 ,P′A=PC=1,∠BP′A=∠BPC,
,P′A=PC=1,∠BP′A=∠BPC,
∴△BPP′为等腰直角三角形,
∴PP′=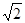 PB=2,∠BP′P=45°,
PB=2,∠BP′P=45°,
在△APP′中,AP=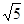 ,PP′=2,AP′=1,
,PP′=2,AP′=1,
∵(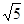 )2=22+12,
)2=22+12,
∴AP2=PP′2+AP′2,
∴△APP′为直角三角形,且∠AP′P=90°
∴∠BP′A=45°+90°=135°,
∴∠BPC=∠BP′A=135°;
(2)∵六边形ABCDEF为正六边形,
∴∠ABC=120°,
把△BPC绕点B逆时针旋转120°,得到了△BP′A,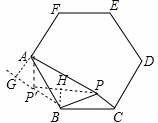
∴∠P′BP=120°,BP′=BP=4,P′A=PC=2,∠BP′A=∠BPC,
∴∠BP′P=∠BPP′=30°,
过B作BH⊥PP′于H,
∵BP′=BP,
∴P′H=PH,
在Rt△BP′H中,∠BP′H=30°,BP′=4,
∴BH=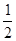 BP′=2,P′H=
BP′=2,P′H= BH=2
BH=2 ,
,
∴P′P=2P′H=4 ,
,
在△APP′中,AP=2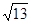 ,PP′=4
,PP′=4 ,AP′=2,
,AP′=2,
∵(2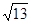 )2=(4
)2=(4 )2+22,
)2+22,
∴AP2=PP′2+AP′2,
∴△APP′为直角三角形,且∠AP′P=90°,
∴∠BP′A=30°+90°=120°,
∴∠BPC=120°,
过A作AG⊥BP′于G点,
∴∠AP′G=60°,
在Rt△AGP′中,AP′=2,∠GAP′=30°,
∴GP′=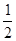 AP′=1,AG=
AP′=1,AG= GP′=
GP′= ,
,
在Rt△AGB中,GB=GP′+P′B=1+4=5,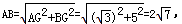
即正六边形ABCDEF的边长为2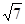 .
.
考点:旋转的性质,正方形的性质、等腰直角三角形的判定与性质、勾股定理与逆定理,含30°的直角三角形的性质
点评:解题的关键是熟记旋转的性质:旋转前后两图形全等,即对应角相等,对应线段相等;对应点与旋转中心的连线段的夹角等于旋转角.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案并作如下约定:
①速度v>0.表示汽车向数轴正方向行驶;
速度v<0,表示汽车向数轴负方向行驶;
速度v=0,表示汽车静止.
②汽车位置在数轴上的坐标s>0,表示汽车位于零千米路标的右侧;
汽车位置在数轴上的坐标s<0,表示汽车位于零千米路标的左侧;
汽车位置在数轴上的坐标s=0,表示汽车恰好位于零千米路标处.
遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图象的形式画在了同一直角坐标系中,如图
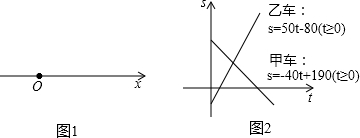
请解答下列问题:
(1)就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格.
| 行驶方向 | 速度的大小(km/h) | 出发前的位置 | |
| 甲车 | |||
| 乙车 |








