题目内容
阅读下列解题过程:
在进行含根号的式子的运算时,我们有时会碰上如
一类的式子,其实我们可以将其进一步化简,如:
=
=
=
-
以上这种化简的步骤叫做分母有理化.
请回答下列问题:
(1)观察上面的解题过程,请化简
;
(2)利用上面提供的信息,求:
+
+
+…+
的值.
在进行含根号的式子的运算时,我们有时会碰上如
| 2 | ||||
|
| 2 | ||||
|
2×(
| ||||||||
(
|
2(
| ||||
(
|
| 5 |
| 3 |
以上这种化简的步骤叫做分母有理化.
请回答下列问题:
(1)观察上面的解题过程,请化简
| 3 | ||||
|
(2)利用上面提供的信息,求:
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
考点:分母有理化
专题:阅读型
分析:1)根据二次根式的乘法,分子分母都乘以分母这两个数的差,可分母有理化;
(2)根据分母有理化,可得实数的减法,根据实数的减法运算,可得答案.
(2)根据分母有理化,可得实数的减法,根据实数的减法运算,可得答案.
解答:(6分)
(1)
=
=
-
;
(2)利用上面提供的信息请化简,得
+
+
+…+
=
-1+
-
+
-
+…+
-
=
-1
(1)
| 3 | ||||
|
3(
| ||||||||
(
|
=
| 5 |
| 2 |
(2)利用上面提供的信息请化简,得
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2015 |
| 2014 |
| 2015 |
点评:本题考查了分母有理化,分子分母都乘以分母这两个数的差进行分母有理化是解题关键.

练习册系列答案
相关题目
下面说法错误的是( )
| A、两点确定一条直线 |
| B、同角的补角相等 |
| C、等角的余角相等 |
| D、射线AB也可以写作射线BA |
若关于x的
=
无实数解,则m的值是( )
| x-1 |
| x+4 |
| m |
| x+4 |
| A、5 | B、-5 | C、1 | D、-1 |
已知x-3y=3,则5-x+3y的值是( )
| A、8 | B、2 | C、-2 | D、-8 |
 如图的几何体中,它的俯视图是( )
如图的几何体中,它的俯视图是( )A、 |
B、 |
C、 |
D、 |
若代数式x2+3y+5的值为8,那么代数式2x2+6y-2的值是等于( )
| A、4 | B、5 | C、6 | D、7 |
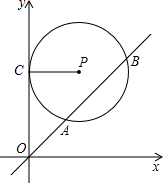 如图,在平面直角坐标系xOy中,⊙P与y轴相切于点C,⊙P的半径是4,直线y=x被⊙P截得的弦AB的长为
如图,在平面直角坐标系xOy中,⊙P与y轴相切于点C,⊙P的半径是4,直线y=x被⊙P截得的弦AB的长为