Question

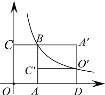
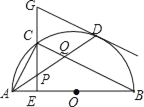
【题目】如图，在平面直角坐标系中，抛物线与轴相交于原点和点，点在抛物线上．

（1）求抛物线的表达式，并写出它的对称轴；

（2）求的值．

Answer 1

【答案】（1），它的对称轴为：；（2）2

【解析】

（1）把点，点分别代入，求出和的值，即可得到抛物线的表达式，根据抛物线的对称轴公式即可求出它的对称轴，

（2）把点代入，求出的值，得到点的坐标，过点作，交于点，过点作，交于点，根据三角形的面积和勾股定理，求出线段和的长，即可得到答案．

解：（1）把点，点分别代入得：

，

解得：，

即抛物线的表达式为：，

它的对称轴为：；

（2）把点代入得：

，

即点的坐标为：（3，3），

过点作，交于点，过点作，交于点，如下图所示，

，

，

，

，

，

．

故答案为：（1），它的对称轴为：x=2；（2）2.