题目内容
如图,矩形AOBC的两边OC、OA分别位于x轴、y轴上,点B的坐标为(- ,2
,2 ),D是CB边上的一点,将△CDO沿直线OD翻折,使C点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .
),D是CB边上的一点,将△CDO沿直线OD翻折,使C点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .
【答案】分析:作EF⊥CO于F,构造相似三角形△EOF和△BOC,利用勾股定理求出OB的长,根据相似三角形的性质求出EF的长,利用勾股定理求出OF的长,得到E的坐标,再利用待定系数法求出函数解析式.
解答: 解:作EF⊥CO于F.
解:作EF⊥CO于F.
∵点B的坐标为(- ,2
,2 ),
),
∴OB= =5,
=5,
∵OE=OC= ,
,
∴ ,即
,即 ,
,
∴EF=2.
在Rt△EFO中,
∵OF= =1,
=1,
∴E(-1,2),代入函数解析式y= 得,k=2×(-1)=-2,
得,k=2×(-1)=-2,
∴函数解析式为y=- .
.
点评:此题主要考查了利用待定系数法求反比例函数关系式,折叠的性质,勾股定理,三角函数的应用,解决问题的关键是利用相似三角形的性质与勾股定理求出E点坐标.
解答:
 解:作EF⊥CO于F.
解:作EF⊥CO于F.∵点B的坐标为(-
 ,2
,2 ),
),∴OB=
 =5,
=5,∵OE=OC=
 ,
,∴
 ,即
,即 ,
,∴EF=2.
在Rt△EFO中,
∵OF=
 =1,
=1,∴E(-1,2),代入函数解析式y=
 得,k=2×(-1)=-2,
得,k=2×(-1)=-2,∴函数解析式为y=-
 .
.点评:此题主要考查了利用待定系数法求反比例函数关系式,折叠的性质,勾股定理,三角函数的应用,解决问题的关键是利用相似三角形的性质与勾股定理求出E点坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
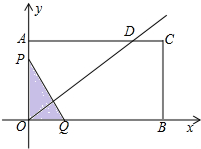
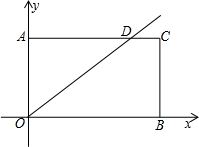 (备用图)
(备用图) 已知:如图,矩形AOBC的两边在坐标轴上,边长AO为2、OB为3,双曲线y=
已知:如图,矩形AOBC的两边在坐标轴上,边长AO为2、OB为3,双曲线y= (2007•郑州模拟)如图,矩形AOBC的两边OC、OA分别位于x轴、y轴上,点B的坐标为(-
(2007•郑州模拟)如图,矩形AOBC的两边OC、OA分别位于x轴、y轴上,点B的坐标为(- (2013•淄博)如图,矩形AOBC的面积为4,反比例函数
(2013•淄博)如图,矩形AOBC的面积为4,反比例函数 的图象经过C,求双曲线和直线AB的解析式.
的图象经过C,求双曲线和直线AB的解析式.