��Ŀ����
��ͼ������AOBC�Ķ���O������ԭ�㣬��OB��OA�ֱ���x��y����������ϣ���OA=6����λ���ȣ�OB=10����λ���ȣ�����y=| 3 | 4 |
��1���߶�AD=
��2���ֱ���0��t��3��7��t��10ʱ��S��t�ĺ�����ϵʽ��
��3�����POQ�����S��������DCBO���һ��ʱt��ֵ��
��4�����˶���ȫ�����У��Ƿ����t��ֵ��ʹ��POQΪ���������Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
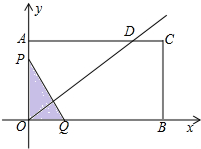
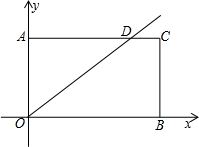 ������ͼ��
������ͼ��
��������1�����D������Ϊ��x��6�����ߵ�D��y=
x�ϣ���x=8����AD=8�����ù��ɶ��������OD=10��
��2��0��t��3ʱ��P��AO�ϣ�Q��OB�ϣ���ʱ��POQΪֱ�������Σ���ֱ�DZ߷ֱ�Ϊt��2t������������7��t��10ʱ��P��DO�ϣ�Q��OB�ϣ������OQΪt•OP�ij��ȣ����á�POM=��ADO������ֵ�������OQ���ϵĸ�PM��
��3�����������BCDO�����Ϊ36����ô�á�POQ���������18��Ӧ��P��AO�ϣ�Q��BO�ϣ�P��AD�ϣ�Q��OB�ϣ�P��DO�ϣ�Q��CB�ϣ�P��DO�ϣ�Q��BC�ϵ����������
��4��P��AO�ϣ�Q��BO�ϣ���ʱΪֱ�������Σ���ֱ�DZߵı߳���������ȣ�������Ϊ���������ε���ʽ��P��AD�ϣ�Q��OB�ϣ�PO=PQ����ʱ��AP�ij��ȵ���OQ��һ�룮PQ=OQ���ɵõ�t����һֵ��P��DO�ϣ�Q��CB�Ͽ�����PO=OQ�õ�t��ֵ��PQ=OP����ʱOM=MQ��P��DO�ϣ�Q��BC�ϡ�POQ�Ƕ۽������Σ������ڵ��������ε������
| 3 |
| 4 |
��2��0��t��3ʱ��P��AO�ϣ�Q��OB�ϣ���ʱ��POQΪֱ�������Σ���ֱ�DZ߷ֱ�Ϊt��2t������������7��t��10ʱ��P��DO�ϣ�Q��OB�ϣ������OQΪt•OP�ij��ȣ����á�POM=��ADO������ֵ�������OQ���ϵĸ�PM��
��3�����������BCDO�����Ϊ36����ô�á�POQ���������18��Ӧ��P��AO�ϣ�Q��BO�ϣ�P��AD�ϣ�Q��OB�ϣ�P��DO�ϣ�Q��CB�ϣ�P��DO�ϣ�Q��BC�ϵ����������
��4��P��AO�ϣ�Q��BO�ϣ���ʱΪֱ�������Σ���ֱ�DZߵı߳���������ȣ�������Ϊ���������ε���ʽ��P��AD�ϣ�Q��OB�ϣ�PO=PQ����ʱ��AP�ij��ȵ���OQ��һ�룮PQ=OQ���ɵõ�t����һֵ��P��DO�ϣ�Q��CB�Ͽ�����PO=OQ�õ�t��ֵ��PQ=OP����ʱOM=MQ��P��DO�ϣ�Q��BC�ϡ�POQ�Ƕ۽������Σ������ڵ��������ε������
����⣺��1��AD=8��OD=10��2�֣�
��2����0��t��3ʱ��S=t2����4�֣�
��7��t��10ʱ��PO=24-2t��
PM=
��24-2t����
S=-
t2+
t
=-
(t-6)2+
��6�֣�


��3����3��t��7ʱ��S=3t��
��10��t��12ʱ��PQ=24-2t��CD=2��CE=
��BE=
��
BQ=t-10��EQ=
-t��NQ=
��
-t����
S=
��12-t����35-2t��
=
t2-
t+168
=
(t-
)2-
3t=18��t=6��
-
t2+
t=18��t=6+
��t=6-
��7���ᣩ����8�֣�
��4��PO=PQ��2t-6=
��
t=4
PQ2=t2-12t+72��PQ2=OQ2��t=6
PO=24-2t��PO=OQ��t=8
OM=
��
��24-2t��=
��
t=
����10�֣�
����


��2����0��t��3ʱ��S=t2����4�֣�
��7��t��10ʱ��PO=24-2t��
PM=
| 3 |
| 5 |
S=-
| 3 |
| 5 |
| 36 |
| 5 |
=-
| 3 |
| 5 |
| 108 |
| 5 |


��3����3��t��7ʱ��S=3t��
��10��t��12ʱ��PQ=24-2t��CD=2��CE=
| 3 |
| 2 |
| 15 |
| 2 |
BQ=t-10��EQ=
| 35 |
| 2 |
| 4 |
| 5 |
| 35 |
| 2 |
S=
| 2 |
| 5 |
=
| 4 |
| 5 |
| 118 |
| 5 |
=
| 4 |
| 5 |
| 59 |
| 4 |
| 121 |
| 20 |
3t=18��t=6��
-
| 3 |
| 5 |
| 36 |
| 5 |
| 6 |
| 6 |
��4��PO=PQ��2t-6=
| t |
| 2 |
t=4
PQ2=t2-12t+72��PQ2=OQ2��t=6
PO=24-2t��PO=OQ��t=8
OM=
| t |
| 2 |
| 4 |
| 5 |
| t |
| 2 |
t=
| 64 |
| 7 |
����



���������⿼���˶��������γ�һ���������һ������״��ע��ֶ���������з�����

��ϰ��ϵ�д�
�����Ŀ
 ��֪����ͼ������AOBC���������������ϣ��߳�AOΪ2��OBΪ3��˫����y=
��֪����ͼ������AOBC���������������ϣ��߳�AOΪ2��OBΪ3��˫����y= ��2007•֣��ģ�⣩��ͼ������AOBC������OC��OA�ֱ�λ��x�ᡢy���ϣ���B������Ϊ��-
��2007•֣��ģ�⣩��ͼ������AOBC������OC��OA�ֱ�λ��x�ᡢy���ϣ���B������Ϊ��- ��2013•�Ͳ�����ͼ������AOBC�����Ϊ4������������
��2013•�Ͳ�����ͼ������AOBC�����Ϊ4������������ ��ͼ��C����˫���ߺ�ֱ��AB�Ľ���ʽ��
��ͼ��C����˫���ߺ�ֱ��AB�Ľ���ʽ��