题目内容
17.已知关于x的一元二次方程(k-2)x2+2x-1=0有两个不相等的实数根,则k的取值范围为( )| A. | k>1 | B. | k>-1且k≠0 | C. | k>1且k≠2 | D. | k<1 |
分析 根据关于x的一元二次方程(k-2)x2+2x-1=0有两个不相等的实数根,可得出判别式大于0,再求得k的取值范围.
解答 解:∵关于x的一元二次方程(k-2)x2+2x-1=0有两个不相等的实数根,
∴△=4+4(k-2)>0,
解得k>-1,
∵k-2≠0,
∴k≠2,
∴k的取值范围k>-1且k≠2,
故选C.
点评 本题考查了根的判别式,总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
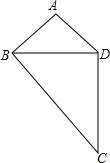 如图,已知AB=4,BC=9,BD=6,$\frac{AD}{DC}$=$\frac{2}{3}$,求证:BD平分∠ABC.
如图,已知AB=4,BC=9,BD=6,$\frac{AD}{DC}$=$\frac{2}{3}$,求证:BD平分∠ABC.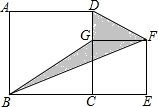 有一个零件的形状如图所示(图中阴影部分),已知图中大正方形的边长为a米,小正方形的边长为b米.
有一个零件的形状如图所示(图中阴影部分),已知图中大正方形的边长为a米,小正方形的边长为b米.