题目内容
如图所示,正方形ABCD边长是2,BE=CE,MN=1,线段MN的端点M、N分别在CD、AD上滑动,当DM= 时,△ABE与以D、M、N为顶点的三角形相似.
【答案】分析:根据题目已知条件发现这两个三角形都是直角三角形,如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.但此题中M、N的点未定,也就是边的对应关系未定,所以需分情况讨论.
解答:解:∵正方形ABCD边长是2
∴BE=CE=1,∠B=∠D=90°
∴在Rt△ABE中,AE= =
=
第一种情况:当△ABE∽△MDN时,AE:MN=AB:DM,即 :1=2:DM,∴DM=
:1=2:DM,∴DM= ;
;
第二种情况:当△ABE∽△NDM时,AE:MN=BE:DM,即 :1=1:DM,∴DM=
:1=1:DM,∴DM= .
.
所以DM= 或
或 .
.
点评:本题考查了直角三角形相似的判定定理,需注意边的对应关系.
解答:解:∵正方形ABCD边长是2
∴BE=CE=1,∠B=∠D=90°
∴在Rt△ABE中,AE=
 =
=
第一种情况:当△ABE∽△MDN时,AE:MN=AB:DM,即
 :1=2:DM,∴DM=
:1=2:DM,∴DM= ;
;第二种情况:当△ABE∽△NDM时,AE:MN=BE:DM,即
 :1=1:DM,∴DM=
:1=1:DM,∴DM= .
.所以DM=
 或
或 .
.点评:本题考查了直角三角形相似的判定定理,需注意边的对应关系.

练习册系列答案
相关题目
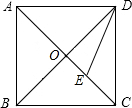 如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )
如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
 4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )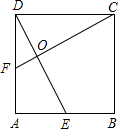 如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF.
如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF. 如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是
如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是 如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: