题目内容
如图所示，△ABC中，∠C=90°，两直角边AC=8，BC=6，在三角形内有一点P，它到各边的距离相等，则这个距离是（ ）分析：根据题意知P点为三角形的内心．已知两条直角边的长度，运用勾股定理可求斜边长度．
根据直角三角形内切圆半径的计算公式 r=
求解．
根据直角三角形内切圆半径的计算公式 r=
| a+b-c |
| 2 |
解答：解：根据题意得 AB=
=
=10．
∴内切圆半径r=
=2．即P点到各边的距离是2．
故选B．
| AC2+BC2 |
| 82+62 |
∴内切圆半径r=
| 8+6-10 |
| 2 |
故选B．
点评：此题考查直角三角形的性质，与三角形的内切圆知识结合起来解答就不难．
练习册系列答案
名校课堂系列答案
相关题目
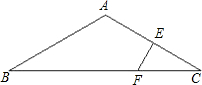如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
16、如图所示，△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、AC于D、E，∠CAE：∠EAB=5：2，则∠B=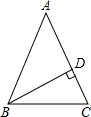
如图所示，△ABC中，AB=AC=10，BD是AC边的高线，DC=2，试求BD的长．
如图所示，△ABC中，BC的垂直平分线交AB于点E，若△ABC的周长为10，BC=4，则△ACE的周长是
如图所示，△ABC中，AB=AC，BD⊥AC，垂足为D，求∠DBC与∠A的关系．