题目内容

如图1，△ABC表示一块含有30°角的直角三角板，30°所对的边AC的长为2，以斜边AB所在直线为x轴，AB边上的高所在直线为y轴，建立平面直角坐标系．
（1）求A、B、C三点的坐标；
（2）求过A、B、C三点的抛物线所对应的二次函数关系式；
（3）如图2，等腰直角△DEF的斜边DE始终在x轴上移动，且DE= $数学公式$ ．问当其直角顶点F的初始位置落在y轴的负半轴时，△DEF经过怎样的平移后点F才落在（1）中的抛物线上？

（1）解：在Rt△ABC中，
∵∠CBA=30°，AC=2，
∴∠CAB=60°，AB=4，
由勾股定理得：BC=2 $\text{[math]}$ ，
∴在Rt△AOC中，∠ACO=30°，
∴AO=1，CO= $\text{[math]}$ ，
∴BO=AB-AO=3．
∴A（-1，0），B（3，0），C（0， $\text{[math]}$ ），
答：A、B、C三点的坐标分别是（-1，0），（3，0），（0， $\text{[math]}$ ）．

（2）解：根据题意设所求抛物线的关系式为y=a（x-3）（x+1），
∵过点C（0， $\text{[math]}$ ），
∴-3×a= $\text{[math]}$ ，解得a= $\text{[math]}$ ．
∴所求抛物线的关系式为y= $\text{[math]}$ （x-3）（x+1），即y= $\text{[math]}$ x²+ $\text{[math]}$ x+ $\text{[math]}$ ，
答：过A、B、C三点的抛物线所对应的二次函数关系式是y= $\text{[math]}$ x²+ $\text{[math]}$ x+ $\text{[math]}$ ．

（3）解：在等腰Rt△DEF中，
∵DE=2 $\text{[math]}$ ，
即：OF= $\text{[math]}$ ，
∴F（0，- $\text{[math]}$ ）
当y=- $\text{[math]}$ ，
∴ $\text{[math]}$ （x-3）（x+1）=- $\text{[math]}$ ．解得x₁= $\text{[math]}$ ，x₂= $\text{[math]}$ ．
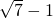∴△DEF向右平移（ $\text{[math]}$ ）个单位或者向左平移（ $\text{[math]}$ ）个单位，点F才落在（1）中的抛物线上，
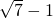答：当其直角顶点F的初始位置落在y轴的负半轴时，△DEF经过向右平移（ $\text{[math]}$ ）个单位或者向左平移（ $\text{[math]}$ ）个单位后，点F才落在（1）中的抛物线上．
分析：（1）根据含30°的直角三角形性质和勾股定理求出AC和AB的长，在Rt△AOC，同理可求出AO、CO的长，即可得到答案；
（2）根据题意设所求抛物线的关系式为y=a（x-3）（x+1），把C的坐标代入就能求出a的值，即可求出抛物线的解析式；
（3）根据等腰Rt△DEF的性质，能求出F的坐标，因为平移，所以点的纵坐标与F的纵坐标相等，把y=- $\text{[math]}$ 代入抛物线的解析式即可求出x的值，就能得到答案．
点评：本题考查对用待定系数法求二次函数的解析式，等腰三角形的性质，含30度角的直角三角形的性质，三角形的内角和定理，勾股定理，解一元二次方程等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键，此题是一个综合性比较强的题目，题型较好．