题目内容
已知等腰△ABC中,AD⊥BC于点D,且AD= BC,则△ABC底角的度数为
BC,则△ABC底角的度数为
- A.45°
- B.75°
- C.45°或75°或15°
- D.60°
C
分析:首先根据题意画出图形,注意分别从∠BAC是顶角与∠BAC是底角去分析,然后利用等腰三角形与直角三角形的性质,即可求得答案.
解答: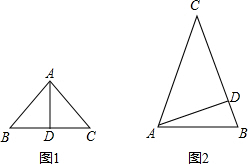 解:如图1:AB=AC,
解:如图1:AB=AC,
∵AD⊥BC,
∴BD=CD= BC,∠ADB=90°,
BC,∠ADB=90°,
∵AD= BC,
BC,
∴AD=BD,
∴∠B=45°,
即此时△ABC底角的度数为45°;
如图2,AC=BC,
∵AD⊥BC,
∴∠ADC=90°,
∵AD= BC,
BC,
∴AD= AC,
AC,
∴∠C=30°,
∴∠CAB=∠B= =75°,
=75°,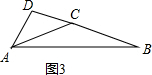
即此时△ABC底角的度数为75°;
如图3,AD⊥BC,AD= BC=
BC= AC,
AC,
∴∠ACD=30°,
∴∠ACB=150°,
∴∠CAB=∠CBA=15°,
∴此时△ABC底角的度数为15°;
综上,△ABC底角的度数为45°或75°或15°.
故选C.
点评:此题考查了等腰三角形的性质、直角三角形的性质以及三角形内角和定理.此题难度适中,注意数形结合思想与分类讨论思想的应用是解此题的关键.
分析:首先根据题意画出图形,注意分别从∠BAC是顶角与∠BAC是底角去分析,然后利用等腰三角形与直角三角形的性质,即可求得答案.
解答:
 解:如图1:AB=AC,
解:如图1:AB=AC,∵AD⊥BC,
∴BD=CD=
 BC,∠ADB=90°,
BC,∠ADB=90°,∵AD=
 BC,
BC,∴AD=BD,
∴∠B=45°,
即此时△ABC底角的度数为45°;
如图2,AC=BC,
∵AD⊥BC,
∴∠ADC=90°,
∵AD=
 BC,
BC,∴AD=
 AC,
AC,∴∠C=30°,
∴∠CAB=∠B=
 =75°,
=75°,
即此时△ABC底角的度数为75°;
如图3,AD⊥BC,AD=
 BC=
BC= AC,
AC,∴∠ACD=30°,
∴∠ACB=150°,
∴∠CAB=∠CBA=15°,
∴此时△ABC底角的度数为15°;
综上,△ABC底角的度数为45°或75°或15°.
故选C.
点评:此题考查了等腰三角形的性质、直角三角形的性质以及三角形内角和定理.此题难度适中,注意数形结合思想与分类讨论思想的应用是解此题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;
24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度; 12、如图:已知等腰△ABC中,腰AB=AC=13cm,底BC=24cm,求△ABC的面积.
12、如图:已知等腰△ABC中,腰AB=AC=13cm,底BC=24cm,求△ABC的面积.