题目内容
【题目】![]() 是
是![]() 的高.
的高.
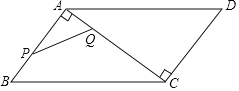
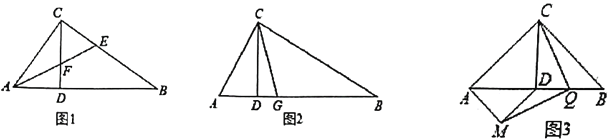
(1)如图1,若![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
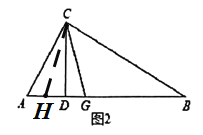
(2)如图2,若![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
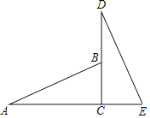
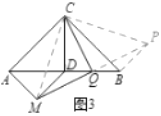
(3)如图3,若![]() 是以
是以![]() 为斜边的等腰直角三角形,再以
为斜边的等腰直角三角形,再以![]() 为斜边作等腰
为斜边作等腰![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() ,试判断线段
,试判断线段![]() 与
与![]() 的关系,并给出证明.
的关系,并给出证明.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据角平分线的定义得到∠CAE=∠BAE,根据同角的余角相等得到∠ACD=∠B,根据三角形的外角性质得到∠CFE=∠CEF,得到CE=CF;
(2)在AD上取点H,使DH=DG,连接CH,证明BC=BH,计算即可;
(3)作MN⊥AB于N,证明△CDQ≌△QNM,根据全等三角形的性质证明即可.
(1)证明:∵![]() 平分
平分![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() 是
是![]() 的高,
的高,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)解:在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,
∵![]() ,
,
可得![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)解:![]() ;
;
证明:延长![]() 至点
至点![]() 使
使![]() ,连接
,连接![]() ,
,
在![]() 和
和![]() 中,
中,
∵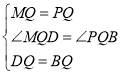 ,
,
∴![]() ≌
≌![]() (
(![]() ),
),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵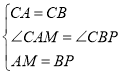 ,
,
∴![]() ≌
≌![]() (
(![]() ),
),
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ;
;
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目