题目内容
 如图直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=4,点P在边AB上滑动,若△DAP与△PBC相似,且AP=3,则PB=________.
如图直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=4,点P在边AB上滑动,若△DAP与△PBC相似,且AP=3,则PB=________.
6或
分析:要使两个三角形相似,则可能是△APD∽△BPC,也可能是△APD∽△BCP,所以应分两种情况讨论,进而求解AP的值即可.
解答:可设PB的长为x,
假设△APD∽△BPC,则 =
= ,
,
即 =
= ,解得x=6;
,解得x=6;
当△APD∽△BCP时,则 =
= ,
,
即 =
= ,解得x=
,解得x= .
.
故答案为:6或 .
.
点评:本题主要考查了相似三角形的判定及性质问题,利用相似三角形的性质得出比例式是解题关键.

分析:要使两个三角形相似,则可能是△APD∽△BPC,也可能是△APD∽△BCP,所以应分两种情况讨论,进而求解AP的值即可.
解答:可设PB的长为x,
假设△APD∽△BPC,则
 =
= ,
,即
 =
= ,解得x=6;
,解得x=6;当△APD∽△BCP时,则
 =
= ,
,即
 =
= ,解得x=
,解得x= .
.故答案为:6或
 .
.点评:本题主要考查了相似三角形的判定及性质问题,利用相似三角形的性质得出比例式是解题关键.

练习册系列答案
相关题目
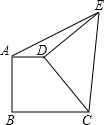 如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )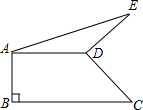 如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=1,BC=3,以D为旋转中心,CD逆时针旋转90°得DE,则AE=
如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=1,BC=3,以D为旋转中心,CD逆时针旋转90°得DE,则AE=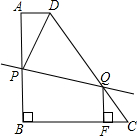 如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.
如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10. 如图直角梯形ABCD的中位线EF的长为a,垂直于底的腰AB长为b,则图中阴影部分的面积为( )
如图直角梯形ABCD的中位线EF的长为a,垂直于底的腰AB长为b,则图中阴影部分的面积为( )