题目内容
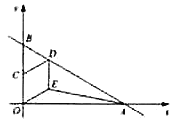
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,四边形
上一点,四边形![]() 是菱形,则
是菱形,则![]() 的面积为______.
的面积为______.
【答案】8![]() .
.
【解析】
已知直线y=![]() x+8与x轴、y轴分别交于A,B两点, 可求得点A、B的坐标分别为:(8
x+8与x轴、y轴分别交于A,B两点, 可求得点A、B的坐标分别为:(8![]() ,0)、(0,8);又因 C是OB的中点, 可得点C(0,4),所以菱形的边长为4,根据菱形的性质可得DE=4=DC,设点D(m,
,0)、(0,8);又因 C是OB的中点, 可得点C(0,4),所以菱形的边长为4,根据菱形的性质可得DE=4=DC,设点D(m,![]() m+8),则点E(m,
m+8),则点E(m,![]() m+4),由两点间的距离公式可得CD2=m2+(
m+4),由两点间的距离公式可得CD2=m2+(![]() m+8﹣4)2=16, 解方程求得m=2
m+8﹣4)2=16, 解方程求得m=2![]() , 即可得点E(2
, 即可得点E(2![]() ,2), 再根据S△OAE=
,2), 再根据S△OAE=![]() ×OA×yE即可求得
×OA×yE即可求得![]() 的面积.
的面积.
∵直线y=![]() x+8与x轴、y轴分别交于A,B两点,
x+8与x轴、y轴分别交于A,B两点,
∴当x=0时,y=8;当y=0时,x=8![]() ,
,
∴点A、B的坐标分别为:(8![]() ,0)、(0,8),
,0)、(0,8),
∵C是OB的中点,
∴点C(0,4),
∴菱形的边长为4,则DE=4=DC,
设点D(m,![]() m+8),则点E(m,
m+8),则点E(m,![]() m+4),
m+4),
则CD2=m2+(![]() m+8﹣4)2=16,
m+8﹣4)2=16,
解得:m=2![]() ,
,
故点E(2![]() ,2),
,2),
S△OAE=![]() ×OA×yE=
×OA×yE=![]() ×8
×8![]() ×2=8
×2=8![]() ,
,
故答案为8![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
画板的边长(dm) | 10 | 20 |
出售价(元/张) | 160 | 220 |
(1)求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?