题目内容
在四边形纸片ABCD中，∠A=70°，∠B=80°．现将纸片的一角对折，使点C落在△ABC内，若∠1=30°，则∠2的度数为30°
30°
．分析：根据折叠的性质得到∠3=∠4，∠5=∠6，利用四边形的内角和为360°得到∠3+∠5+∠C+∠D=360°，∠A+∠B+∠C+∠D=360°，则∠3+∠5=∠A+∠B=70°+80°=150°，∠4+∠6=150°，由
∠1+∠4+∠2+∠6+∠A+∠B=360°可得∠1+∠2=360°-150°×2=60°，然后把∠1=30°代入计算即可得到∠2的度数．
∠1+∠4+∠2+∠6+∠A+∠B=360°可得∠1+∠2=360°-150°×2=60°，然后把∠1=30°代入计算即可得到∠2的度数．
解答：解：如图，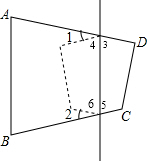
根据题意得∠3=∠4，∠5=∠6，
∵∠3+∠5+∠C+∠D=360°，
而∠A+∠B+∠C+∠D=360°，
∴∠3+∠5=∠A+∠B=70°+80°=150°，
∴∠4+∠6=150°，
∵∠1+∠4+∠2+∠6+∠A+∠B=360°，
∴∠1+∠2=360°-150°×2=60°，
而∠1=30°，
∴∠2=30°．
故答案为30°．
根据题意得∠3=∠4，∠5=∠6，∵∠3+∠5+∠C+∠D=360°，
而∠A+∠B+∠C+∠D=360°，
∴∠3+∠5=∠A+∠B=70°+80°=150°，
∴∠4+∠6=150°，
∵∠1+∠4+∠2+∠6+∠A+∠B=360°，
∴∠1+∠2=360°-150°×2=60°，
而∠1=30°，
∴∠2=30°．
故答案为30°．
点评：本题考查了多边形的内角和定理：n边形的内角和为（n-2）•180°．也考查了折叠的性质．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，在四边形纸片ABCD中，AD∥BC，AB∥CD，将纸片折叠，点A、D分别落在A′、D′处，且A′D′经过点B，EF为折痕，若∠D′FC=86°时，∠A′EB=（ ）
