题目内容
在△ABC中,D为AB边上一点,过点D作DE∥BC交AC于点E,以DE为折线,将△ADE翻折,设所得的△A′DE与梯形DBCE重叠部分的面积为y.(1)如图(甲),若∠C=90°,AB=10,BC=6,
| AD |
| AB |
| 1 |
| 3 |
(2)如图(乙),若AB=AC=10,BC=12,D为AB中点,则y的值为
(3)若∠B=30°,AB=10,BC=12,设AD=x.
①求y与x的函数解析式;
②y是否有最大值?若有,求出y的最大值;若没有,请说明理由.

分析:(1)本题需先根据已知条件得出AC的长,再根据DE∥BC得出△ADE∽△ABC,再根据面积之比等于相似比的平方即可求出结果.
(2)本题需先根据已知条件得出BC边上的高的值和S△ABC的值,再根据D为AB中点和DE∥BC,即可得出△ADE∽△ABC,最后根据面积之比等于相似比的平方即可求出结果;
(3)本题需先作AH⊥BC于点H,根据已知条件得出AH和S△ABC的值,再分两种情况0<x≤5时和当5<x<10进行讨论,分别求出S△A′DE和S△MA′N的值,即可求出y的最大值.
(2)本题需先根据已知条件得出BC边上的高的值和S△ABC的值,再根据D为AB中点和DE∥BC,即可得出△ADE∽△ABC,最后根据面积之比等于相似比的平方即可求出结果;
(3)本题需先作AH⊥BC于点H,根据已知条件得出AH和S△ABC的值,再分两种情况0<x≤5时和当5<x<10进行讨论,分别求出S△A′DE和S△MA′N的值,即可求出y的最大值.
解答:解:(1)∵∠C=90°,AB=10,BC=6,
∴AC=8,
∴S△ABC=
×6×8=24,
∵DE∥BC,
∴△ADE∽△ABC,
∴
=(
)2,
∴
=
,
∵S△ADE=
,
∴y=
;
(2)∵AB=AC=10,BC=12,
∴BC边上的高为8,
∴S△ABC=
×12×8=48,
∵D为AB的中点,DE∥BC,
∴△ADE∽△ABC,
=
,
∴
=(
)2,
∴
=
,
∴S△ADE=12,
∴y=12;
(3)如图,作AH⊥BC于点H,在Rt△ABH中,
∵∠B=30°,AB=10,BC=12,
∴AH=5,S△ABC=
BC•AH=30.
当点A′落在BC上时,点D是AB的中点,即x=5.
故分以下两种情况讨论:
①当0<x≤5时,如图,
∵DE∥BC,
∴△ADE∽△ABC.
∴
=(
)2=(
)2=
.
∴S△A′DE=S△ADE=
×30=
x2.即y=
x2.
∴当x=5时,y最大=
×52=
.
②当5<x<10时,如上图,设DA′、EA′分别交BC于M、N.
由折叠知,△A′DE≌△ADE,
∴DA′=DA=x,∠1=∠2.
∵DE∥BC,
∴∠1=∠B,∠2=∠3.
∴∠B=∠3.
∴DM=DB=10-x.
∴MA′=x-(10-x)=2x-10.
由①同理可得S△DA′E=
x2.又△MA′N∽△DA′E,
∴
=(
)2.
∴S△MA′N=
x2•(
)2=
(x-5)2.
∴y=S△DA'E-S△MA'N=-
x2+12x-30=-
(x-
)2+10.
∵二次项系数-
<0,且当x=
时,满足5<x<10,
∴y最大=10.
综上所述,当x=
时,y值最大,最大值是10.
∴AC=8,
∴S△ABC=
| 1 |
| 2 |
∵DE∥BC,
∴△ADE∽△ABC,
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
∴
| S△ADE |
| 24 |
| 1 |
| 9 |
∵S△ADE=
| 8 |
| 3 |
∴y=
| 8 |
| 3 |
(2)∵AB=AC=10,BC=12,
∴BC边上的高为8,
∴S△ABC=
| 1 |
| 2 |
∵D为AB的中点,DE∥BC,
∴△ADE∽△ABC,
| AD |
| AB |
| 1 |
| 2 |
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
∴
| S△ADE |
| 48 |
| 1 |
| 4 |
∴S△ADE=12,
∴y=12;
(3)如图,作AH⊥BC于点H,在Rt△ABH中,
∵∠B=30°,AB=10,BC=12,
∴AH=5,S△ABC=
| 1 |
| 2 |

当点A′落在BC上时,点D是AB的中点,即x=5.
故分以下两种情况讨论:
①当0<x≤5时,如图,
∵DE∥BC,
∴△ADE∽△ABC.
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
| x |
| 10 |
| x2 |
| 100 |
∴S△A′DE=S△ADE=
| x2 |
| 100 |
| 3 |
| 10 |
| 3 |
| 10 |
∴当x=5时,y最大=
| 3 |
| 10 |
| 15 |
| 2 |
②当5<x<10时,如上图,设DA′、EA′分别交BC于M、N.
由折叠知,△A′DE≌△ADE,
∴DA′=DA=x,∠1=∠2.
∵DE∥BC,
∴∠1=∠B,∠2=∠3.
∴∠B=∠3.
∴DM=DB=10-x.
∴MA′=x-(10-x)=2x-10.
由①同理可得S△DA′E=
| 3 |
| 10 |
∴
| S△MA′N |
| S△DA′E |
| 2x-10 |
| x |
∴S△MA′N=
| 3 |
| 10 |
| 2x-10 |
| x |
| 6 |
| 5 |
∴y=S△DA'E-S△MA'N=-
| 9 |
| 10 |
| 9 |
| 10 |
| 20 |
| 3 |
∵二次项系数-
| 9 |
| 10 |
| 20 |
| 3 |
∴y最大=10.
综上所述,当x=
| 20 |
| 3 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有函数解析式的求法和求y的最大值,在求有关最大值问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
 已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积.
已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积.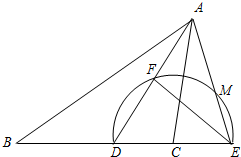 AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.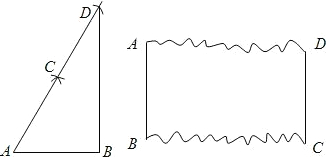
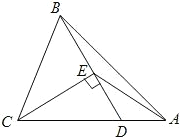
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.