题目内容
 如图,点C在△ADE的边DE上,AD与BC相交于点F,∠1=∠2,
如图,点C在△ADE的边DE上,AD与BC相交于点F,∠1=∠2,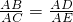 .
.
(1)试说明:△ABC∽△ADE;
(2)试说明:AF•DF=BF•CF.
(1)证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
∵ =
= ,
,
∴ =
=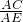 ,
,
∴△ABC∽△ADE;
(2)证明:∵△ABC∽△ADE,
∴∠B=∠D,
∵∠BFA=∠DFC,
∴△ABF∽△CDF,
∴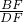 =
= ,
,
∴AF•DF=BF•CF.
分析:(1)求出∠BAC=∠DAE,根据有两组对应边的比相等,且这两边的夹角也相等的两三角形相似推出即可;
(2)根据相似三角形的性质推出∠B=∠D,根据相似三角形的判定推出△ABF∽△CDF,推出比例式,即可得出答案.
点评:本题主要考查了相似的性质和判定的应用,注意:①相似三角形的对应边的比相等;②有两组对应边的比相等,且这两边的夹角也相等的两三角形相似.
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
∵
 =
= ,
,∴
 =
=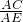 ,
,∴△ABC∽△ADE;
(2)证明:∵△ABC∽△ADE,
∴∠B=∠D,
∵∠BFA=∠DFC,
∴△ABF∽△CDF,
∴
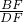 =
= ,
,∴AF•DF=BF•CF.
分析:(1)求出∠BAC=∠DAE,根据有两组对应边的比相等,且这两边的夹角也相等的两三角形相似推出即可;
(2)根据相似三角形的性质推出∠B=∠D,根据相似三角形的判定推出△ABF∽△CDF,推出比例式,即可得出答案.
点评:本题主要考查了相似的性质和判定的应用,注意:①相似三角形的对应边的比相等;②有两组对应边的比相等,且这两边的夹角也相等的两三角形相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,点C在△ADE的边DE上,AD与BC相交于点F,∠1=∠2,
如图,点C在△ADE的边DE上,AD与BC相交于点F,∠1=∠2,
 ,请说明△ABC∽△ADE.
,请说明△ABC∽△ADE.