��Ŀ����
����Ŀ�������꣬ȫ���Կ�����Ⱦ����Խ��Խ���ӣ�����������������Ҳ���������ӣ�ij�̳��ӳ��ҹ�����A��B�����ͺŵĿ��������������־����������������Ϣ������
A������������̨�� | B������������̨�� | ������Ԫ�� |
5 | 3 | 950 |
3 | 4 | 900 |
��1��ÿ̨A�Ϳ�����������B�Ϳ�������������������ֱ��Ƕ��٣�
��2���ù�˾�ƻ�һ�ι��������ͺŵĿ�����������80̨������B�Ϳ����������Ľ�����������A�Ϳ�����������2����Ϊʹ�ù�˾��������80̨�������������������������������Ӧ�Ľ���������
��3����֪A�Ϳ����������ľ�������Ϊ200m3/Сʱ��B�Ϳ����������ľ�������Ϊ300m3/Сʱ��ij���������ڻ���ص������Ϊ200m2������ǽ��3m���ó��ظ����˼ƻ�����5̨����������ÿ�컨��30���ӽ����ڿ�������һ�£��������ǿ������������أ�����Ҫ����A�Ϳ�������������̨��
���𰸡���1��ÿ̨A�Ϳ�����������B�Ϳ�������������������ֱ���100Ԫ��150Ԫ����2������������3��3̨��
��������
��1��������������г���Ӧ�ķ����飬�Ӷ��������ÿ̨A�Ϳ�����������B�Ϳ�������������������ֱ��Ƕ���Ԫ��
��2������������Եõ��������A�Ϳվ���������֮��ĺ�����ϵ���Ӷ����Խ���⣻
��3���������⣬�����г���Ӧ�IJ���ʽ���Ӷ����Խ���⣮
�⣺��1����ÿ̨A�Ϳ�����������B�Ϳ�������������������ֱ���xԪ��yԪ��
![]() ����
����![]() ��
��
��ÿ̨A�Ϳ�����������B�Ϳ�������������������ֱ���100Ԫ��150Ԫ��
��2���蹺��A�ͺŵĿ���������ą������B�ͺŵĿ�����������80��a��̨������ΪwԪ��
w��100a+150��80��a������50a+12000��
��B�Ϳ����������Ľ�����������A�Ϳ�����������2����
��80��a��2a��
��ã�a��![]() ��
��
����a��27ʱ��wȡ�����ֵ����ʱw��10650��80��a��53��
�𣺵�����A�ͺŵĿ���������27̨������B�ͺŵĿ���������53̨ʱ������ʹ�ù�˾��������80̨����������������������
��3���蹺��A�Ϳ���������b̨������B�Ϳ�����������5��b��̨��
200b��![]() +300����5��b����
+300����5��b����![]() ��200��3��
��200��3��
��ã�b��3��
�������A�Ϳ���������3̨��
������Ҫ����A�Ϳ���������3̨��

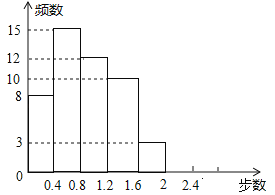
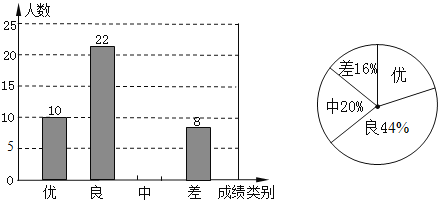
����Ŀ���ֽ����˶�����Խ��Խ����˹�ע��ϲ����ij��ȤС���������������50����ʦij�ա����˶����еIJ������������ͳ�����������������µ�ͳ��ͼ�������������������������Ϣ�������������
��1��д��a��b��ֵ����ȫƵ���ֲ�ֱ��ͼ��
��2��50����ʦ���ա����˶���ͳ�������в�������λ�����ڵ��� ���飻����Լ��40000����ʦ�����������߲�������1.2������1.2���Ľ�ʦԼ���� ������
��3������50��������Ľ�ʦ�У�ѡȡ�����߲�������16000��������16000������������ʦ���ҷ����ĵã���ѡȡ��������ʦǡ�ö���2000��������20000�����ϵĸ��ʣ�
�������� | Ƶ�� | Ƶ�� |
0��x��0.4 | 8 | a |
0.4��x��0.8 | 15 | 0.3 |
0.8��x��1.2 | 12 | 0.241 |
1.2��x��1.6 | 10 | 0.2 |
1.6��x��2 | 3 | 0.06 |
2��x��2.4 | b | 0.04 |