题目内容
9.已知一个三角形各边的比为3:4:5,联结各边的中点所得的三角形的周长为52cm,求原三角形各边的长.分析 由中点和中位线定义可得新三角形的各边长为原三角形各边长的一半,即可求其周长.
解答 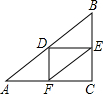 解:如图,D,E,F分别是△ABC的三边的中点,
解:如图,D,E,F分别是△ABC的三边的中点,
则DE=$\frac{1}{2}$AC,DF=$\frac{1}{2}$BC,EF=$\frac{1}{2}$AB,
所以△DEF的周长=DE+DF+EF=$\frac{1}{2}$(AC+BC+AB)=52cm,
所以AC+BC+AB=104.
又因为AC:BC:AB=3:4:5,
所以AC=26cm,BC=$\frac{104}{3}$cm,AB=$\frac{130}{3}$cm.
点评 本题考查了三角形中位线定理.解决本题的关键是利用中点定义和中位线定理得到新三角形各边长与原三角形各边长的数量关系.

练习册系列答案
相关题目
 如图,小亮从A点出发前进5m,向右转15°,再前进5m,又向右转15°…,这样一直走下去,他第一次回到出发点A时,一共走了120m.
如图,小亮从A点出发前进5m,向右转15°,再前进5m,又向右转15°…,这样一直走下去,他第一次回到出发点A时,一共走了120m. 如图,用同样大小的正方形瓷砖铺一块正方形地面,两条对角线铺黑色,其他地方铺白色.铺满这块地面一共用了白色瓷砖100块,那么黑色瓷砖共用了21 块.
如图,用同样大小的正方形瓷砖铺一块正方形地面,两条对角线铺黑色,其他地方铺白色.铺满这块地面一共用了白色瓷砖100块,那么黑色瓷砖共用了21 块.