题目内容
 在△ABC中,AB=AC=5,BC=6,点D为BC边上一动点(不与点B重合),以D为圆心,DC的长为半径作⊙D.当⊙D与AB边相切时,半径DC的长为
在△ABC中,AB=AC=5,BC=6,点D为BC边上一动点(不与点B重合),以D为圆心,DC的长为半径作⊙D.当⊙D与AB边相切时,半径DC的长为考点:切线的性质,相似三角形的判定与性质
专题:
分析:如图,假设AB与⊙D相切于点F,连接FD.通过相似三角形△BFD∽△BGA的对应边成比例得到
=
.DF=6-BD,由勾股定理求得AG=4,BA=5,所以把相关线段的长度代入便可以求得BD的长度.
| DF |
| AG |
| DB |
| BA |
解答:解:如图,假设AB与⊙D相切于点F,连接FD,则DF=DC,∠BFD=90°.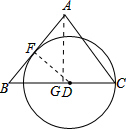
过点A作AG⊥BC于点G,则∠BGA=90°.
∴在△BFD和△BGA中,∠BFD=∠BGA=90°,∠B=∠B,
∴△BFD∽△BGA,
∴
=
.
又∵AB=AC=5,BC=6,AG⊥BC
∴BG=
BC=3,AG=
=4,
∴
=
,
解得BD=
,
∴CD=BC-BD=6-
=
.
故答案为:
.

过点A作AG⊥BC于点G,则∠BGA=90°.
∴在△BFD和△BGA中,∠BFD=∠BGA=90°,∠B=∠B,
∴△BFD∽△BGA,
∴
| DF |
| AG |
| DB |
| BA |
又∵AB=AC=5,BC=6,AG⊥BC
∴BG=
| 1 |
| 2 |
| AB2-BG2 |
∴
| 6-BD |
| 4 |
| BD |
| 5 |
解得BD=
| 10 |
| 3 |
∴CD=BC-BD=6-
| 10 |
| 3 |
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:本题考查了切线的性质、相似三角形的判定和性质以及勾股定理的运用,解题的关键是添加辅助线构造直角三角形.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 实数a在数轴上的位置如图所示,化简
实数a在数轴上的位置如图所示,化简| (3-a)2 |
| (a-1)2 |
| A、4-2a | B、2a-2 |
| C、4 | D、2 |
下列函数关系中,y是x的二次函数的是( )
| A、y=2x+3 | ||
B、y=
| ||
| C、y=x2-1 | ||
D、y=
|
将边长为1的正方形对折5次后,得到的图形面积是( )
| A、0.03125 |
| B、0.0625 |
| C、0.125 |
| D、0.25 |
 如图,在等腰Rt△ABC中,∠C=90°,AC=3,D是AC上一点.若tan∠DBA=
如图,在等腰Rt△ABC中,∠C=90°,AC=3,D是AC上一点.若tan∠DBA=