题目内容
【题目】如图等边△ABC的边长为4cm,点P,点Q同时从点A出发点,Q沿AC以1cm/s的速度向点C运动,点P沿A﹣B﹣C以2cm/s的速度也向点C运动,直到到达点C时停止运动,若△APQ的面积为S(cm2),点Q的运动时间为t(s),则下列最能反映S与t之间大致图象是( )
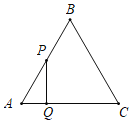
A.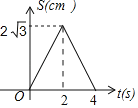 B.
B.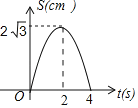
C.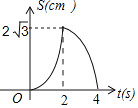 D.
D.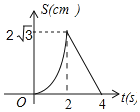
【答案】C
【解析】
根据等边三角形的性质可得,然后根据点P的位置分类讨论,分别求出S与t的函数关系式即可得出结论.
解:∵△ABC为等边三角形
∴∠A=∠C=60°,AB=BC=AC=4
当点P在AB边运动时,
根据题意可得AP=2t,AQ=t
∴△APQ为直角三角形
S=![]() AQ×PQ=
AQ×PQ=![]() AQ×(AP·sinA)=
AQ×(AP·sinA)=![]() ×t×2t×
×t×2t×![]() =
=![]() t2,图象为开口向上的抛物线,
t2,图象为开口向上的抛物线,
当点P在BC边运动时,如下图,
根据题意可得PC=2×4-2t=8-2t,AQ=t
S=![]() ×AQ×PH=
×AQ×PH=![]() ×AQ×(PC·sinC)=
×AQ×(PC·sinC)=![]() ×t×(8﹣2t)×
×t×(8﹣2t)×![]() =
=![]() t(4﹣t)=-
t(4﹣t)=-![]() t2+
t2+![]() ,
,

图象为开口向下的抛物线;
故选:C.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目