题目内容
如图，在矩形ABCD中，AB=4，BC=3，点P在AB边上运动，连接CP，过点D作DQ⊥CP，垂足为Q．设CP=x，DQ=y，则y与x的函数关系式是________．（不必写出x的取值范围）
y=
分析：根据四边形ABCD是矩形，DQ⊥CP，和∠DCP=∠CBP，即可求证△DQC∽△CBP，所以
=
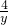即可得到y与x的函数关系式．
解答：∵四边形ABCD是矩形，DQ⊥CP．
∴∠DQC=∠B=90°，
又∵∠DCP=∠CPB，
∴△DQC∽△CBP，
∴
=
，
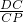∵AB=4，BC=3，CP=x，DQ=y
∴=；
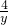∴xy=12，
∴y=．
故答案为：y=．
点评：此题主要考查学生对相似三角形的判定与性质和矩形性质的理解和掌握，此题的关键是利用相似三角形对应边成比例，难度不大，是一道基础题．
分析：根据四边形ABCD是矩形，DQ⊥CP，和∠DCP=∠CBP，即可求证△DQC∽△CBP，所以
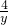=即可得到y与x的函数关系式．解答：∵四边形ABCD是矩形，DQ⊥CP．
∴∠DQC=∠B=90°，
又∵∠DCP=∠CPB，
∴△DQC∽△CBP，
∴
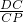=，∵AB=4，BC=3，CP=x，DQ=y
∴
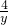=；∴xy=12，
∴y=
．故答案为：y=
．点评：此题主要考查学生对相似三角形的判定与性质和矩形性质的理解和掌握，此题的关键是利用相似三角形对应边成比例，难度不大，是一道基础题．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=4cm，BC=8cm，点P从点A出发以1cm/s的速度向点B运动，点Q从点B出发以2cm/s的速度向点C运动，设经过的时间为xs，△PBQ的面积为ycm2，则下列图象能反映y与x之间的函数关系的是（ ）
．
动过程中，Q点停留了1s，图②是P、Q两点在折线AB-BC-CD上相距的路程S（cm）与时间t（s）之间的函数关系图象．
如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB=60°，AB=6，则AD=（ ）
DE，EF与AB交于点F，设CE=x，BF=y．