题目内容
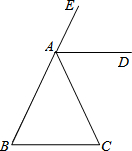如图，△ABC中，∠BAC的外角的平分线AD∥BC．试说明：AB=AC．考点：等腰三角形的判定与性质,平行线的性质
专题：证明题
分析：由平行可得∠EAD=∠B，∠DAC=∠C，结合角平分线，可得∠B=∠C，可得出结论．
解答：证明：∵AD∥BC，
∴∠EAD=∠B，∠DAC=∠C，
∵AD是∠EAC的平分线，
∴∠EAD=∠DAC，
∴∠B=∠C，
∴AB=AC．
∴∠EAD=∠B，∠DAC=∠C，
∵AD是∠EAC的平分线，
∴∠EAD=∠DAC，
∴∠B=∠C，
∴AB=AC．
点评：本题主要考查等腰三角形的判定，由平行和角平分线的定义得到角相等是解题的关键．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
如图，OA=OB，OC=OD，∠O=50°，∠D=35°，则∠DAC等于（ ）| A、60° | B、50° |
| C、85° | D、30° |
函数y=
x2+1与y=
x2+2的图象的不同之处是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、对称轴 | B、开口方向 |
| C、顶点 | D、形状 |
若方程
=
有增根，则a的值为（ ）
| x-1 |
| x-2 |
| a |
| 2-x |
| A、2 | B、1 | C、-2 | D、-1 |
若点P（a，-b）在第三象限，则点M（a，-ab）在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |