Question

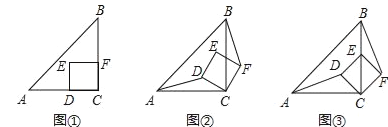
【题目】感知：如图①，△ABC是等腰直角三角形，∠ACB=90°，正方形CDEF的顶点D、F分别在边AC、BC上，易证：AD=BF（不需要证明）；

探究：将图①的正方形CDEF绕点C顺时针旋转α（0°＜α＜90°），连接AD、BF，其他条件不变，如图②，求证：AD=BF；

应用：若α=45°，CD=，BE=1，如图③，则BF=　 　．

Answer 1

【答案】（1）证明见解析；（2）

【解析】试题分析: 探究：证明△ADC≌△BFC，可得结论；

应用：过D作DG⊥AC于G，先根据勾股定理得：EC=2，得正方形边长为3，则AC=3，根据α=45°，得△DCG是等腰直角三角形，求出CG的长，则得AG的长，再次利用勾股定理求AD的长，即BF的长．

试题解析:

证明:探究:如图②，

四边形CDEF为正方形,

∴CD=CF,

由旋转得:∠ACD=∠BCF,

△ABC是等腰直角三角形,∠ACB=90°,

∴AC=BC，

△ADC≌△BFC,

∴AD=BF；

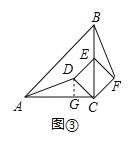
应用:如图③,

∵四边形CDEF为正方形,

∠EDC=90° ED=DC,

,

∴BC=BE+EC=1+2=3,

∴AC=BC=3，

过D作DG⊥AC于G,

∵a=45°,

即∠ACD=45,

∴△DCG是等腰直角三角形,

∴DG=CG=1,

∴AG=BC-CG=3-1=2,

由勾股定理得: ,

同理得:△ADC≌△BFC,

点睛: 本题是四边形和图形旋转的综合题，考查了正方形、等腰直角三角形、全等三角形的性质，熟知正方形的各边相等，各角都是90°，等腰直角三角形的两直角边相等，且锐角为45°；明确旋转角相等，同时利用三角形全等和勾股定理求边和角的度数，使问题得以解决．