题目内容
如图，O为等边三角形ABC内一点，∠OCB=∠ABO，则∠BOC的度数是________．
120°
分析：根据等边三角形的三个角都是60°求出∠ABC=60°，再求出∠OBC+∠OCB=60°，然后根据三角形内角和定理列式计算即可得解．
解答：∵△ABC是等边三角形，
∴∠ABC=60°，
∵∠OCB=∠ABO，
∴∠OBC+∠OCB=∠OBC+∠ABO=∠ABC=60°，
∴在△OBC中，∠BOC=180°-（∠OBC+∠OCB）=180°-60°=120°．
故答案为：120°．
点评：本题考查了等边三角形的性质，三角形的内角和定理，是基础题，熟记等边三角形的每一个内角都是60°是解题的关键．
分析：根据等边三角形的三个角都是60°求出∠ABC=60°，再求出∠OBC+∠OCB=60°，然后根据三角形内角和定理列式计算即可得解．
解答：∵△ABC是等边三角形，
∴∠ABC=60°，
∵∠OCB=∠ABO，
∴∠OBC+∠OCB=∠OBC+∠ABO=∠ABC=60°，
∴在△OBC中，∠BOC=180°-（∠OBC+∠OCB）=180°-60°=120°．
故答案为：120°．
点评：本题考查了等边三角形的性质，三角形的内角和定理，是基础题，熟记等边三角形的每一个内角都是60°是解题的关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
3、如图，△ABC为等边三角形，∠ABC、∠ACB的平分线相交于点O，OE∥AB交BC于点E，OF∥AC交BC于点F，图中等腰三角形共有（ ）
如图，△ABC为等边三角形，点D，E，F分别在AB，BC，CA边上，且△DEF是等边三角形，求证：△ADF≌△CFE．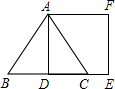
如图，△ABC为等边三角形，AD为BC边上的高，且AB=2，则正方形ADEF的面积为
如图，△ABC为等边三角形，D为△ABC内一点，△ABD逆时针旋转后到达△ACP位置，则∠APD=
如图①，△ABC为等边三角形，周长为p．D1，E1，F1分别是△ABC三边的中点，连接D1E1，E1F1，F1D1，可得△D1E1F1．