题目内容
已知:如图,A(a,m),B(2a,n)是反比例函数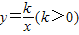 图象上的两点,分别过A,B两点作x轴的垂线,垂足分别为C、D,连接OA,OB.
图象上的两点,分别过A,B两点作x轴的垂线,垂足分别为C、D,连接OA,OB.(1)求证:S△AOC=S△OBD;
(2)若A,B两点又在一次函数
 的图象上,且S△OAB=8,求a的值.
的图象上,且S△OAB=8,求a的值.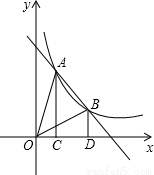
【答案】分析:(1)根据反比例函数图象上点得坐标特点得到am=k,2an=k,再根据三角形面积公式得到S△AOC= OC•AC=
OC•AC= a×m=
a×m= k,S△BOD=
k,S△BOD= OD×BD=
OD×BD= ×2a×n=
×2a×n= k,即可得到结论;
k,即可得到结论;
(2)先把A、B两点坐标代入一次函数解析式,可以用a表示为A点坐标(a,- a+b),B点坐标(2a,-
a+b),B点坐标(2a,- a+b),再利用A、B两点在反比例函数图象上,则k=a•(-
a+b),再利用A、B两点在反比例函数图象上,则k=a•(- a+b)=2a•(-
a+b)=2a•(- a+b),于是解得b=4a,然后用a表示一次函数与坐标轴两交点坐标F(0,4a),E(3a,0),然后利用S△AOB=S△E0F-S△EOA-S△BOF=8和三角形面积公式得到关于a的方程,再解方程可得a的值.
a+b),于是解得b=4a,然后用a表示一次函数与坐标轴两交点坐标F(0,4a),E(3a,0),然后利用S△AOB=S△E0F-S△EOA-S△BOF=8和三角形面积公式得到关于a的方程,再解方程可得a的值.
解答:(1)证明:∵A(a,m),B(2a,n)是反比例函数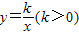 上,且AC⊥OC,BD⊥OD,
上,且AC⊥OC,BD⊥OD,
∴am=k,2an=k,
∵S△AOC= OC•AC=
OC•AC= a×m=
a×m= k,S△BOD=
k,S△BOD= OD×BD=
OD×BD= ×2a×n=
×2a×n= k,
k,
∴S△AOC=S△OBD;
(2)解:∵A,B两点在一次函数y=- x上,
x上,
∴A点坐标可表示为(a,- a+b),B点坐标表示为(2a,-
a+b),B点坐标表示为(2a,- a+b),
a+b),
∵A,B在是反比例函数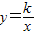 上,
上,
∴a•(- a+b)=2a•(-
a+b)=2a•(- a+b),解得b=4a,
a+b),解得b=4a,
∴A点坐标为(a, a),B点坐标表示为(2a,
a),B点坐标表示为(2a, a),
a),
∵A(a,m),B(2a,n)是反比例函数 上,
上,
∴一次函数 与x轴,y轴的交点F(0,4a),E(3a,0),如图,
与x轴,y轴的交点F(0,4a),E(3a,0),如图,
∵S△AOB=S△E0F-S△FOA-S△BOE=8,
即 •3a•4a-
•3a•4a- 4a•a-
4a•a- •3a•
•3a• a=8,
a=8,
∴a2=4,
∴a=±2(负号舍去)
∴a=2.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数图象与一次函数图象的交点坐标满足两个函数的解析式.也考查了三角形面积公式.
 OC•AC=
OC•AC= a×m=
a×m= k,S△BOD=
k,S△BOD= OD×BD=
OD×BD= ×2a×n=
×2a×n= k,即可得到结论;
k,即可得到结论;(2)先把A、B两点坐标代入一次函数解析式,可以用a表示为A点坐标(a,-
 a+b),B点坐标(2a,-
a+b),B点坐标(2a,- a+b),再利用A、B两点在反比例函数图象上,则k=a•(-
a+b),再利用A、B两点在反比例函数图象上,则k=a•(- a+b)=2a•(-
a+b)=2a•(- a+b),于是解得b=4a,然后用a表示一次函数与坐标轴两交点坐标F(0,4a),E(3a,0),然后利用S△AOB=S△E0F-S△EOA-S△BOF=8和三角形面积公式得到关于a的方程,再解方程可得a的值.
a+b),于是解得b=4a,然后用a表示一次函数与坐标轴两交点坐标F(0,4a),E(3a,0),然后利用S△AOB=S△E0F-S△EOA-S△BOF=8和三角形面积公式得到关于a的方程,再解方程可得a的值.解答:(1)证明:∵A(a,m),B(2a,n)是反比例函数
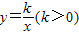 上,且AC⊥OC,BD⊥OD,
上,且AC⊥OC,BD⊥OD,
∴am=k,2an=k,
∵S△AOC=
 OC•AC=
OC•AC= a×m=
a×m= k,S△BOD=
k,S△BOD= OD×BD=
OD×BD= ×2a×n=
×2a×n= k,
k,∴S△AOC=S△OBD;
(2)解:∵A,B两点在一次函数y=-
 x上,
x上,∴A点坐标可表示为(a,-
 a+b),B点坐标表示为(2a,-
a+b),B点坐标表示为(2a,- a+b),
a+b),∵A,B在是反比例函数
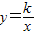 上,
上,∴a•(-
 a+b)=2a•(-
a+b)=2a•(- a+b),解得b=4a,
a+b),解得b=4a,∴A点坐标为(a,
 a),B点坐标表示为(2a,
a),B点坐标表示为(2a, a),
a),∵A(a,m),B(2a,n)是反比例函数
 上,
上,∴一次函数
 与x轴,y轴的交点F(0,4a),E(3a,0),如图,
与x轴,y轴的交点F(0,4a),E(3a,0),如图,∵S△AOB=S△E0F-S△FOA-S△BOE=8,
即
 •3a•4a-
•3a•4a- 4a•a-
4a•a- •3a•
•3a• a=8,
a=8,∴a2=4,
∴a=±2(负号舍去)
∴a=2.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数图象与一次函数图象的交点坐标满足两个函数的解析式.也考查了三角形面积公式.

练习册系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为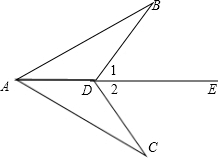 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为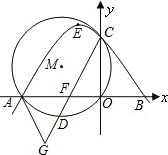 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧