题目内容
【题目】二次函数y=ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（-2，-9a），下列结论：①abc>0；②4a+2b+c<0；③9a-b+c=0；④若方程a（x+5）（x-1）=-1有两个根x1和x2，且x1＜x2，则-5＜x1＜x2＜1；⑤若方程|ax2+bx+c|=1有四个根，则这四个根的和为-8，其中正确的结论有（ ）个．
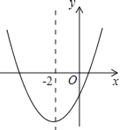
A.2B.3C.4D.5
【答案】B
【解析】
根据开口方向及顶点坐标求出b=4a，c=-5a,可求得①②③，根据图像得平移和韦达定理即可判断④⑤．
解：函数的顶点坐标为(-2，-9a)
则
，
则b=4a，c=-5a
函数开口向上，
a＞0，
则b＞0，c＜0
则abc＜0,①错误
把x=2代入二次函数表达式，则
=7a＞0，②错误
=0，③正确
a（x+5）（x-1）=-1展开后得
函数
向上平移一个单位变成
=
其与x轴的两个交点的横坐标
和
就是方程
的两个解
而与x轴的交点的坐标为(-5，0)，(1，0)
因为y=在的上方，
所以-5＜＜＜1，④正确
化简为
或
的两解为和
由韦达定理
+=
=-4
的两个解设为
和
由韦达定理
+==-4
故+++=-8，⑤正确
故本题答案为B．
【题目】某学校八年级共400名学生，为了解该年级学生的视力情况，从中随机抽取40名学生的视力数据作为样本，数据统计如下：
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图：
等级 | 视力（x） | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
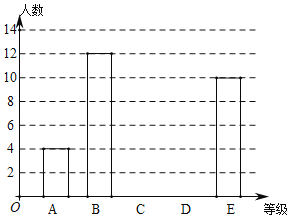
根据上面提供的信息，回答下列问题：
（1）统计表中的
，
；
（2）请补全条形统计图；
（3）根据抽样调查结果，请估计该校八年级学生视力为“
级”的有多少人？
（4）该年级学生会宣传部有2名男生和2名女生，现从中随机挑选2名同学参加“防控近视，爱眼护眼”宣传活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．
