题目内容
3.正方形ABCD的边长为4,点P在正方形ABCD的边上,BP=5,则CP=3或$\sqrt{17}$..分析 根据点P的位置不同分两种情况.①当点P在AD上时,根据正方形的性质利用勾股定理即可求出BP、DP的长度解答;②当点P在CD上时,根据正方形的性质利用勾股定理即可求出CP即可得出结论.
解答 解:点P的位置分两种情况(如图所示):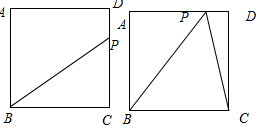
①当点P在CD上时,
∵四边形ABCD为正方形,
∴∠C=90°,
∵BC=4,BP=5,
∴CP=3;
②当点P在AD上时,
∵四边形ABCD为正方形,
∴∠A=90°,
∵AB=4,BP=5,
∴AP=3,
∴DP=1,
∵四边形ABCD为正方形,
∴∠D=90°,
∵CD=4,DP=1,
∴CP=$\sqrt{17}$.
故答案为:3或$\sqrt{17}$.
点评 本题考查了正方形的性质、勾股定理,解题的关键是分两种情况考虑.本题属于中档题,难度不大,解决该题型题目时,根据点的位置不同分情况考虑是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.根据下列条件,能判定△ABC≌△A′B′C′的是( )
| A. | AB=A′B′,BC=B′C′,∠A=∠A′ | B. | ∠A=∠A′,∠B=∠B′,AC=B′C′ | ||
| C. | ∠A=∠A′,∠B=∠B′,∠C=∠C′ | D. | AB=A′B′,BC=B′C′,AC=A′C′ |
12.下列对正方形的描述错误的是( )
| A. | 正方形的四个角都是直角 | B. | 正方形的对角线互相垂直 | ||
| C. | 邻边相等的矩形是正方形 | D. | 对角线相等的平行四边形是菱形 |
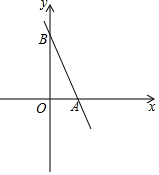 如图,直线y=-2x+3与x轴相交于点A,与y轴相交于点B.
如图,直线y=-2x+3与x轴相交于点A,与y轴相交于点B.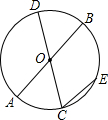 如图,AB、CD是⊙O的直径,弦CE∥AB,弧$\widehat{CE}$的度数为50°,求∠AOC的度数.
如图,AB、CD是⊙O的直径,弦CE∥AB,弧$\widehat{CE}$的度数为50°,求∠AOC的度数. 画出图中几何体的三视图.
画出图中几何体的三视图.