题目内容
是否存在实数m,使关于x的方程2x2+mx+5=0的两实根的平方的倒数和等于 ?若存在,求出m;若不存在,说明理由.
?若存在,求出m;若不存在,说明理由.
解:设原方程的两根为x1、x2,
则有: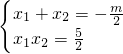 ,
,
∴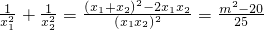 .
.
又∵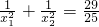 ,
,
∴m2-20=29,解得m=±7,
∴△=m2-4×2×5=m2-40=(±7)2-40=9>0
∴存在实数±7,使关于原方程的两实根的平方的倒数和等于 .
.
分析:根据根与系数的关系,两实根的平方的倒数和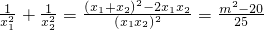 .
.
即可确定m的取值情况.
点评:利用根与系数的关系和根的判别式来解决.容易出现的错误是忽视所求的m的值是否满足判别式△.
则有:
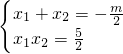 ,
,∴
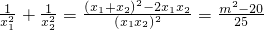 .
.又∵
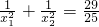 ,
,∴m2-20=29,解得m=±7,
∴△=m2-4×2×5=m2-40=(±7)2-40=9>0
∴存在实数±7,使关于原方程的两实根的平方的倒数和等于
 .
.分析:根据根与系数的关系,两实根的平方的倒数和
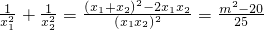 .
.即可确定m的取值情况.
点评:利用根与系数的关系和根的判别式来解决.容易出现的错误是忽视所求的m的值是否满足判别式△.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目