题目内容
已知矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8cm,则该矩形的面积为 .
考点:矩形的性质
专题:
分析:根据∠AOD=120°,可得∠AOB=60°,则△AOB为等边三角形,由AC=8cm,得AB=4cm,由勾股定理得,BC=4
cm,再求出矩形的面积即可.
| 3 |
解答:解:∵∠AOD=120°,可得∠AOB=60°,
∵AO=BO=CO=DO,AC=8cm,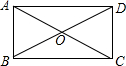
∴AB=4cm,
∵∠ABC=90°,
∴∠ACB=30°,
∴BC=
=4
cm,
∴矩形的面积=4×4=16
cm2.
故答案为16
cm2.
∵AO=BO=CO=DO,AC=8cm,

∴AB=4cm,
∵∠ABC=90°,
∴∠ACB=30°,
∴BC=
| AC2-AB2 |
| 3 |
∴矩形的面积=4×4=16
| 3 |
故答案为16
| 3 |
点评:本题考查了矩形的对角线平分且相等的性质,注意勾股定理的熟练应用.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线 如图,△ABC中,∠C=90°,CD是AB上的中线,AB=10,则CD=
如图,△ABC中,∠C=90°,CD是AB上的中线,AB=10,则CD=