��Ŀ����
����Ŀ������������������ͬһ���Ա���x����Ӧ�ĺ���ֵ�ֱ�Ϊ![]() ����ǡ����
����ǡ����![]() �����yΪ
�����yΪ![]() ������ֵ������.
������ֵ������.
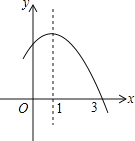
��1����![]() ��ͼ��Ϊֱ�ߣ�
��ͼ��Ϊֱ�ߣ�![]() ��ͼ���������ߣ������ǵ���ֵ������ͼ��Ϊ�� ��
��ͼ���������ߣ������ǵ���ֵ������ͼ��Ϊ�� ��
A.ֱ�� B.������ C.˫���� D.���ϴ𰸾���
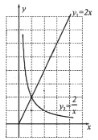
��2����![]() �����ǵ���ֵ����Ϊ
�����ǵ���ֵ����Ϊ![]() ��
��
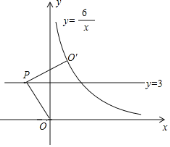
������P��![]() ��
��![]() �����ǵ���ֵ����ͼ���ϣ����P������Ϊ_________.
�����ǵ���ֵ����ͼ���ϣ����P������Ϊ_________.
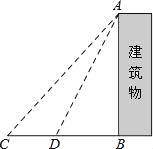
������ͼ�У�����������ֵ�����Ĵ���ͼ��.������ͼ��д�������ֵ�������������ʣ�
����1��_______________________________��
����2��_______________________________��
��������ֵ����������˵�������Ϊ1�ij����Σ����ó����γ�������ʱ���ܳ���С.
���𰸡���1��B����2���٣�1��2����������1����x=1ʱ����ֵ����y��ֵ��СΪ2��
����2����0<x<1ʱ����ֵ����y��x���������С���ۼ����
��������
��1������������![]() �������
�������![]() ���ж�y�ĺ���ͼ��
���ж�y�ĺ���ͼ��
��2���ٸ��ݵ�P��![]() ��
��![]() �����ǵ���ֵ����ͼ���ϣ��������̼��������P�����ꣻ�ڸ�����ֵ��������ʽ��������ͼ����ͼ��۲켴�ɵó����ʼ��ɣ����賤Ϊx�����Ϊ
�����ǵ���ֵ����ͼ���ϣ��������̼��������P�����ꣻ�ڸ�����ֵ��������ʽ��������ͼ����ͼ��۲켴�ɵó����ʼ��ɣ����賤Ϊx�����Ϊ![]() �����ܳ�
�����ܳ�![]() ��������ֵ�������ʼ������.
��������ֵ�������ʼ������.
�⣺��1����������![]()
��![]()
![]()
��y��Ȼ�Ƕ��κ�������ֵ������ͼ��Ϊ������
��ѡB��
��2����![]() ��P��
��P��![]() ��
��![]() �����ǵ���ֵ����ͼ����
�����ǵ���ֵ����ͼ����
��![]() ���
���![]()
��![]()
���P��������1��2����
�ڸ��ݺ�������ʽ������ͼ�����£�

����1����x=1ʱ����ֵ����y��ֵ��СΪ2��
����2����0<x<1ʱ����ֵ����y��x���������С��
��3���賤Ϊx�����Ϊ![]() �����ܳ�
�����ܳ�![]()
����ֵ�����Ķ����֪��cΪ![]() ����ֵ����
����ֵ����
�����ʿ�֪����![]() ��
��![]() ʱ��cȡ����Сֵ
ʱ��cȡ����Сֵ
��![]()
��![]() ��-1��ȥ��
��-1��ȥ��
���ij�����Ϊ������ʱ���ܳ���С.

 ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д�