题目内容
如图,△ABC是圆O的内接三角形,AB是直径,∠ABC=45°,点M在边AC上,点N在边BC上,△MCN与△MPN关于直线MN对称,P是AB上的点.
(1)当点P是边AB的中点时,求证: ;
;
(2)当点P不是边AB的中点时, 是否仍然成立?请证明你的结论.
是否仍然成立?请证明你的结论.

(1)证明:连接CP,依据题意得折痕MN⊥CP.
∵AC=BC,AP=BP,
∴CP⊥AB.
∴MN∥AB,
∴ .
.
∴ .
.

(2)解:当点P不是斜边AB的中点时, 仍然成立.
仍然成立.
证明如下:
连接CP,则MN⊥CP.作PE⊥AC于E.
∵∠ACB=90°,
∴PE∥BC,
∴ .
.
又AC=BC,∠A=∠B=45°,∠APE=∠B=45°,
∴AE=PE.
∵∠MCN=90°,CP⊥MN,
∴∠ECP=∠MNC,
∴Rt△MCN∽Rt△PEC,
∴ .
.
∴ .
.
∴ .
.
分析:(1)连接CP,依据题意得折痕MN⊥CP,由AC=BC,AP=BP,可得CP⊥AB,MN∥AB,利用平行线分线段成比例定理,即可证得 ;
;
(2)连接CP,则MN⊥CP.作PE⊥AC于E,易得PE∥BC,由平行线分线段成比例定理与等腰三角形的性质,即可证得Rt△MCN∽Rt△PEC,由相似三角形的对应边成比例,即可证得答案.
点评:此题考查了翻折变换的性质,平行线分线段成比例定理,相似三角形的判定与性质等知识.此题难度适中,解题时要注意比例变形与数形结合思想的应用.
∵AC=BC,AP=BP,
∴CP⊥AB.
∴MN∥AB,
∴
 .
.∴
 .
.
(2)解:当点P不是斜边AB的中点时,
 仍然成立.
仍然成立.证明如下:
连接CP,则MN⊥CP.作PE⊥AC于E.
∵∠ACB=90°,
∴PE∥BC,
∴
 .
.又AC=BC,∠A=∠B=45°,∠APE=∠B=45°,
∴AE=PE.
∵∠MCN=90°,CP⊥MN,
∴∠ECP=∠MNC,
∴Rt△MCN∽Rt△PEC,
∴
 .
.∴
 .
.∴
 .
.分析:(1)连接CP,依据题意得折痕MN⊥CP,由AC=BC,AP=BP,可得CP⊥AB,MN∥AB,利用平行线分线段成比例定理,即可证得
 ;
;(2)连接CP,则MN⊥CP.作PE⊥AC于E,易得PE∥BC,由平行线分线段成比例定理与等腰三角形的性质,即可证得Rt△MCN∽Rt△PEC,由相似三角形的对应边成比例,即可证得答案.
点评:此题考查了翻折变换的性质,平行线分线段成比例定理,相似三角形的判定与性质等知识.此题难度适中,解题时要注意比例变形与数形结合思想的应用.

练习册系列答案
相关题目
 如图,△ABC是圆内接正三角形,P为劣弧BC上一点,已知AB=
如图,△ABC是圆内接正三角形,P为劣弧BC上一点,已知AB= 如图.△ABC是圆的内接正三角形,D是BC弧上任意一点,试探求线段BD、DC、DE之间的关系并予证明.
如图.△ABC是圆的内接正三角形,D是BC弧上任意一点,试探求线段BD、DC、DE之间的关系并予证明.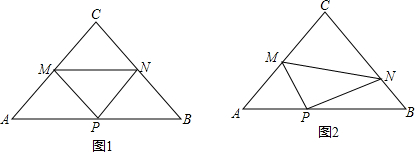
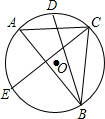 如图,△ABC是圆O的内接三角形,且AB≠AC,∠ABC和∠ACB的平分线,分别交圆O于点D,E,且BD=CE,则∠A等于( )
如图,△ABC是圆O的内接三角形,且AB≠AC,∠ABC和∠ACB的平分线,分别交圆O于点D,E,且BD=CE,则∠A等于( ) ,PA=6.
,PA=6.