题目内容
 如图.△ABC是圆的内接正三角形,D是BC弧上任意一点,试探求线段BD、DC、DE之间的关系并予证明.
如图.△ABC是圆的内接正三角形,D是BC弧上任意一点,试探求线段BD、DC、DE之间的关系并予证明.
分析:延长CD至H,使DH=BD,△ABC为正三角形,然后可证△ABD≌△CBH,得BD+DC=HC=AD,利用(同弧所对的圆周角相等)求△ABD∽△CED,然后利用其对应边成比例即可证明.
解答: 解:
解:
+
=
证明:延长CD至H,使DH=BD,△ABC为正三角形,
∴∠BDC=120°,∠BDH=180°-∠BDC=60°,
∴△DBH为正三角形,
∴BD=HD,∠H=60°,
又∵AB=BC,∠ADB=∠ACB=60°,∠BAD=∠BCD,
∴△ABD≌△CBH,
∴AD=HC=HD+DC=BD+DC,
又∵∠DCE=∠BAD,∠EDC=∠ADB,(同弧所对的圆周角相等)
∴△ABD∽△CED
∴
=
∴
=
,
∴
=
∴
+
=
.
 解:
解:| 1 |
| BD |
| 1 |
| DC |
| 1 |
| DE |
证明:延长CD至H,使DH=BD,△ABC为正三角形,
∴∠BDC=120°,∠BDH=180°-∠BDC=60°,
∴△DBH为正三角形,
∴BD=HD,∠H=60°,
又∵AB=BC,∠ADB=∠ACB=60°,∠BAD=∠BCD,
∴△ABD≌△CBH,
∴AD=HC=HD+DC=BD+DC,
又∵∠DCE=∠BAD,∠EDC=∠ADB,(同弧所对的圆周角相等)
∴△ABD∽△CED
∴
| AD |
| BD |
| DC |
| DE |
∴
| BD+DC |
| BD |
| DC |
| DE |
∴
| BD+DC |
| BD?DC |
| 1 |
| DE |
∴
| 1 |
| BD |
| 1 |
| DC |
| 1 |
| DE |
点评:此题考查学生对相似三角形的判定与性质,全等三角形的判定与性质,等边三角形的判定与性质,圆周角定理等知识点的理解和掌握,综合性较强,难度较大.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
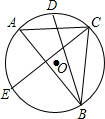 如图,△ABC是圆O的内接三角形,且AB≠AC,∠ABC和∠ACB的平分线,分别交圆O于点D,E,且BD=CE,则∠A等于( )
如图,△ABC是圆O的内接三角形,且AB≠AC,∠ABC和∠ACB的平分线,分别交圆O于点D,E,且BD=CE,则∠A等于( )
 如图.△ABC是圆的内接正三角形,D是BC弧上任意一点,试探求线段BD、DC、DE之间的关系并予证明.
如图.△ABC是圆的内接正三角形,D是BC弧上任意一点,试探求线段BD、DC、DE之间的关系并予证明.