题目内容
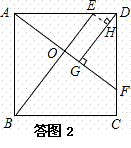
如图13所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G。
[1]求证:AF⊥BE;
[2]试探究线段AO、BO、GO的长度之间的数量关系;
[3]若GO:CF=4:5,试确定E点的位置。
 |
[1]证明:∵![]() ABCD为正方形,且DE=CF,
ABCD为正方形,且DE=CF,
∴AE=DF,AB=AD,∠BAE=∠ADF=90°,
∴△ABE≌△DAF,
∴∠ABE=∠DAF,又∵∠ABE+∠AEB=90°![]() ,
,
 ∴∠DAF+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AOE=90°,即AF⊥BE;
[2]解:BO=A![]() O+OG.
O+OG.
理由:由[1]的结论可知,
∠ABE=∠DAF,∠AOB=∠DGA=90°,AB=AD,
则△ABO≌△DAG,
所以,BO=AG=AO+OG;
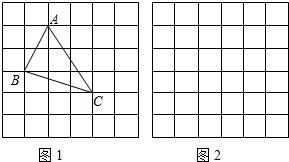
[3]解:过E点作EH⊥DG,垂足为H[如答图2所示],
由矩形的性质,得EH=OG,
∵DE=CF,GO:CF=4:5,∴EH:ED=4:5,
∵AF⊥BE,AF⊥DG,∴OE∥DG,
∴∠AEB=∠EDH,△ABE∽△HED,
∴AB:BE=EH:ED=4:5,
在Rt△ABE中,AE:AB=3:4,
故AE:AD=3:4,
即AE= [![]() 3AD]/4。
3AD]/4。

练习册系列答案
相关题目
 点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.