题目内容
在平面直角坐标系xOy中,直线y=kx-2k+6经过定点Q.
(1)直接写出点Q的坐标 ;
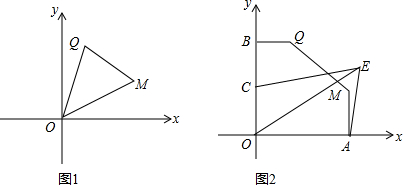
(2)点M在第一象限内,∠QOM=45°,若点M的横坐标与点Q的纵坐标相等(如图1),求直线QM的解析式;
(3)在(2)条件下,过点M作MA⊥x轴于点A,过点Q作QB⊥y轴于点B,点E为第一象限内的一动点,∠AEO=45°,点C为OB的中点(如图2),求线段CE长度的最大值.
(1)直接写出点Q的坐标
(2)点M在第一象限内,∠QOM=45°,若点M的横坐标与点Q的纵坐标相等(如图1),求直线QM的解析式;
(3)在(2)条件下,过点M作MA⊥x轴于点A,过点Q作QB⊥y轴于点B,点E为第一象限内的一动点,∠AEO=45°,点C为OB的中点(如图2),求线段CE长度的最大值.

考点:一次函数综合题
专题:
分析:(1)y=kx-2k+6=k(x-2)+6,则当x-2=0,即x=2时,y的值与k无关,据此即可求得G的坐标;
(2)延长BQ,AM交于点F.连接OF,作QG⊥OF于点G,证明△OQG∽△OMA,根据相似三角形的对应边的比相等,即可求得AE的长,则E的坐标可以求得,然后利用待定系数法即可求解;
(3)E在圆心在OA的上边,且弦OA所对的圆心角是90°的圆上,据此即可求得圆心的坐标,从而求解.
(2)延长BQ,AM交于点F.连接OF,作QG⊥OF于点G,证明△OQG∽△OMA,根据相似三角形的对应边的比相等,即可求得AE的长,则E的坐标可以求得,然后利用待定系数法即可求解;
(3)E在圆心在OA的上边,且弦OA所对的圆心角是90°的圆上,据此即可求得圆心的坐标,从而求解.
解答:解:(1)y=kx-2k+6=k(x-2)+6,
则当x-2=0,即x=2时,y的值与k无关,
则G的坐标是(2,6);
(2)延长BQ,AM交于点F.连接OF,作QG⊥OF于点G.
则四边形AOBF是正方形,△QFG是等腰直角三角形,且OA=OB=BF=AF=6,BQ=2,
则QF=4,
∴QG=QF×
=4×
=2
,
在直角△OBQ中,OQ=
=
=2
,
∴直角△OQG中,OG=
=
=4
.
∵正方形AOBF中,∠AOB=90°,∠AOF=45°,
又∵∠QOM=45°,
∴∠QOG+∠FOM=∠FOM+∠AOM=45°,
∴∠QOG=∠AOM,
又∵∠OGQ=∠AOM
∴△OQG∽△OMA,
∴
=
,即
=
,
∴AM=4,
∴M的坐标是(6,4).
设直线QM的解析式是y=kx+b,
则
,
解得:
,
则直线的解析式是:y=-
x+7;
(3)∵∠AEO=45°,
∴E在圆心在OA的上边,且弦OA所对的圆心角是90°的圆上,设圆心是N,则N的坐标是(3,3),圆的半径是3
,
又∵点C为OB的中点,
∴C的坐标是(0,3),
则CN∥x轴,
则当E是CN的延长线与圆N的交点时,线段CE最长,则最大的长度是:3+3
.
则当x-2=0,即x=2时,y的值与k无关,
则G的坐标是(2,6);
(2)延长BQ,AM交于点F.连接OF,作QG⊥OF于点G.
则四边形AOBF是正方形,△QFG是等腰直角三角形,且OA=OB=BF=AF=6,BQ=2,
则QF=4,
∴QG=QF×
| ||
| 2 |
| ||
| 2 |
| 2 |
在直角△OBQ中,OQ=
| OB2+BQ2 |
| 62+22 |
| 10 |
∴直角△OQG中,OG=
| OQ2-QG2 |
| 40-8 |
| 2 |
∵正方形AOBF中,∠AOB=90°,∠AOF=45°,

又∵∠QOM=45°,
∴∠QOG+∠FOM=∠FOM+∠AOM=45°,
∴∠QOG=∠AOM,
又∵∠OGQ=∠AOM
∴△OQG∽△OMA,
∴
| QG |
| AM |
| OG |
| OA |
2
| ||
| AM |
4
| ||
| 8 |
∴AM=4,
∴M的坐标是(6,4).
设直线QM的解析式是y=kx+b,
则
|
解得:
|
则直线的解析式是:y=-
| 1 |
| 2 |
(3)∵∠AEO=45°,
∴E在圆心在OA的上边,且弦OA所对的圆心角是90°的圆上,设圆心是N,则N的坐标是(3,3),圆的半径是3
| 2 |
又∵点C为OB的中点,
∴C的坐标是(0,3),
则CN∥x轴,
则当E是CN的延长线与圆N的交点时,线段CE最长,则最大的长度是:3+3
| 2 |
点评:本题考查了一次函数、正方形的性质以及相似三角形的判定与性质的综合应用,正确证明△OQG∽△OMA,以及确定E的位置是关键.

练习册系列答案
相关题目
下列各式一定成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下表是某校在一次体检中所抽取的八年级20名女生身高统计结果:( )
则该班被抽取的女生身高的众数和平均数(保留两位小数)分别是( )
| 身高/m | 1.51 | 1.52 | 1.53 | 1.54 | 1.55 | 1.56 | 1.57 |
| 人数 | 1 | 1 | 3 | 4 | 3 | 6 | 2 |
| A、1.54m,1.56m |
| B、1.55m,1.54m |
| C、1.53m,1.55m |
| D、1.56m,1.55m |
 已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).
已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).