题目内容
化简：（1）
，其中1＜x＜2；
（2）
解：（1）原式=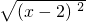
+|1-x|=|x-2|+|1-x|
因为x-2＜0，1-x＜0，
所以原式=2-x+x-1=1．
（2）∵
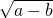有意义，
∴a＞b，
∴原式=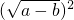
-|a-b|-|a-b|
=a-b-a+b-a+b=b-a．
分析：（1）把x2-4x+4写成完全平方式，利用二次根式的性质去根号加绝对值，然后根据x的范围去绝对值，最后合并即可；
（2）先得到a＞b，然后根据此条件化简二次根式和去绝对值，最后合并即可．
点评：本题考查了二次根式的性质和二次根式的化简：二次根式
（a≥0）；
．同时考查了绝对值的意义．
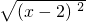+|1-x|=|x-2|+|1-x|因为x-2＜0，1-x＜0，
所以原式=2-x+x-1=1．
（2）∵
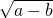有意义，∴a＞b，
∴原式=
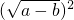-|a-b|-|a-b|=a-b-a+b-a+b=b-a．
分析：（1）把x2-4x+4写成完全平方式，利用二次根式的性质去根号加绝对值，然后根据x的范围去绝对值，最后合并即可；
（2）先得到a＞b，然后根据此条件化简二次根式和去绝对值，最后合并即可．
点评：本题考查了二次根式的性质和二次根式的化简：二次根式
（a≥0）；．同时考查了绝对值的意义． 
练习册系列答案
开心蛙状元测试卷系列答案
相关题目