题目内容
1.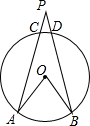 如图,点P为⊙O外一点,点A、B在圆上,PA、PB交优弧AB于点C、D,若∠AOB=60°,则判断∠APB大小正确的是( )
如图,点P为⊙O外一点,点A、B在圆上,PA、PB交优弧AB于点C、D,若∠AOB=60°,则判断∠APB大小正确的是( )| A. | ∠APB=30° | B. | ∠APB>30° | C. | ∠APB<30° | D. | 不能确定 |
分析 连接BC,已知∠AOB=60°,∠AOB与∠ACB为优弧AB所对的圆心角和圆周角,利用圆周角定理求得∠ACB,再利用三角形外角的性质得出答案即可.
解答 解:如图,
∵∠AOB与∠ACB为优弧AB所对的圆心角和圆周角,
∴∠ACB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°=30°,
∵∠ACB是△PBC的外角,
∴∠APB<∠ACB=30°.
故选:C.
点评 本题考查了圆周角定理的运用,三角形外角的性质,掌握同弧所对的圆心角和圆周角之间的关系是解决问题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列各数中是无理数的是( )
| A. | 8 | B. | $\root{3}{27}$ | C. | $\frac{13}{5}$ | D. | $\sqrt{5}$ |
13.某班开展跳绳比赛,5名同学的成绩如下(单位:个):137,140,142,138,140,这组数据的中位数是( )
| A. | 137 | B. | 138 | C. | 140 | D. | 142 |
 如图有三点A、B、C,请按照下列语句画出图形.
如图有三点A、B、C,请按照下列语句画出图形. 如图,以已知线段AB为弦作⊙O,使其经过已知点C.利用直尺和圆规作图(保留作图痕迹,不必写出作法).
如图,以已知线段AB为弦作⊙O,使其经过已知点C.利用直尺和圆规作图(保留作图痕迹,不必写出作法).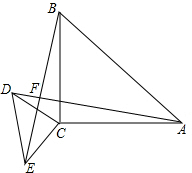 已知△ABC与△CDE都是等腰直角三角形,∠ACB=90°,∠DCE=90°,连结BE,AD,相交于点F.求证:
已知△ABC与△CDE都是等腰直角三角形,∠ACB=90°,∠DCE=90°,连结BE,AD,相交于点F.求证: 实数a、b、c在数轴上的对应点如图所示,化简$|{b-a}|+\sqrt{{{({b-c})}^2}}-\sqrt{a^2}$.
实数a、b、c在数轴上的对应点如图所示,化简$|{b-a}|+\sqrt{{{({b-c})}^2}}-\sqrt{a^2}$.