Question

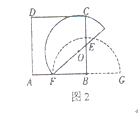
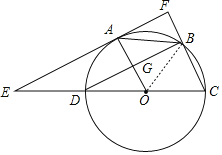
【题目】如图，已知⊙的直径，为圆周上两点，且四边形是平行四边形，直线切⊙于点，分别交的延长线于点，与交于点.

(1)求证：；

(2)求的长.

Answer 1

【答案】(1)证明见解析；(2)AE=.

【解析】

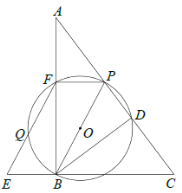
（1）利用圆周角定理得到∠DBC=90°，再利用平行四边形的性质得AO∥BC，所以BD⊥OA，再根据切线的性质得出OA⊥EF，所以OA⊥EF，于是得到EF∥BD；

（2）连接OB，如图，利用平行四边形的性质得OA=BC，则OB=OC=BC，于是可判断△OBC为等边三角形，所以∠C=60°，易得∠AOE=∠C=60°，然后在Rt△OAE中利用正切的定义可求出AE的长．

解：(1) ：∵CD为直径，

∴∠DBC=90°，

∴BD⊥BC，

∵四边形OABC是平行四边形，

∴AO∥BC，

∴BD⊥OA，

∵直线EF切⊙O于点A，

∴OA⊥EF，

∴EF∥BD；

(2)连接,

∵四边形OABC是平行四边形，

∴OA=BC，

而OB=OC=OA，

∴OB=OC=BC，

∴△OBC为等边三角形，

∴∠C=60°，

∴∠AOE=∠C=60°，

在Rt△OAE中，，

.