题目内容
18.现有A、B两枚均匀的骰子(骰子的每个面上分别标有数字1,2,3,4,5,6).以小莉掷出A骰子正面朝上的数字为x、小明掷出B骰子正面朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P在已知抛物线y=-x2+5x上的概率为( )| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{6}$ |
分析 画树状图展示所有36种等可能的结果数,再利用二次函数图象上点的坐标特征,找出点P在抛物线y=-x2+5x上的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有36种等可能的结果数,点P在抛物线y=-x2+5x上的结果数为4,
所以点P在已知抛物线y=-x2+5x上的概率=$\frac{4}{36}$=$\frac{1}{9}$.
故选C.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图,在等边△ABC中,AB=2$\sqrt{2}$,以点A为圆心,AB为半径画$\widehat{BD}$,使得∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
如图,在等边△ABC中,AB=2$\sqrt{2}$,以点A为圆心,AB为半径画$\widehat{BD}$,使得∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
 如图,在等边△ABC中,AB=2$\sqrt{2}$,以点A为圆心,AB为半径画$\widehat{BD}$,使得∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
如图,在等边△ABC中,AB=2$\sqrt{2}$,以点A为圆心,AB为半径画$\widehat{BD}$,使得∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )| A. | π-2 | B. | π-1 | C. | 2π-2 | D. | 2π+1 |
13.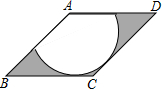 如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
 如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )| A. | 1-$\frac{3\sqrt{2}π}{16}$ | B. | $\sqrt{2}-\frac{3π}{8}$ | C. | 1-$\frac{3π}{8}$ | D. | $\frac{3π}{8}$ |
3. 如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )
如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )
 如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )
如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )| A. | 100 | B. | 81 | C. | 64 | D. | 49 |
10.下列计算正确的是( )
| A. | a3+a3=a6 | B. | 3a2÷a2=2a2 | C. | (a3)2=a5 | D. | a•a2=a3 |
8.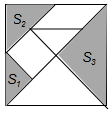 有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
 有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )| A. | 1:2:3 | B. | 1:$\sqrt{2}$:2 | C. | 1:$\sqrt{2}$:4 | D. | 1:2:4 |
 已知正方形纸 ABCD 的面积是 50cm 2,将四个角分别沿虚线往里折叠得到一个较小的正方形 EFGH ( E,F,G,H 分别为各边中点).
已知正方形纸 ABCD 的面积是 50cm 2,将四个角分别沿虚线往里折叠得到一个较小的正方形 EFGH ( E,F,G,H 分别为各边中点).