Question

【题目】在平面直角坐标系中，点到封闭图形的“极化距离”定义如下：任取图形上一点，记长度的最大值为，最小值为（若与重合，则），则“极化距离”．

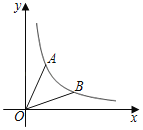
（1）如图1，正方形以原点为中心，点的坐标为，

①点到线段的“极化距离”_______；

点到线段的“极化距离”_________；

②记正方形为图形，点在轴上，且，求点的坐标；

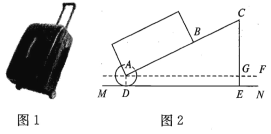
（2）如图2，图形为圆心在轴上，半径为的圆，直线与轴，轴分别交于，两点，若线段上的任一点都满足，直接写出圆心的横坐标的取值范围．

Answer 1

【答案】（1）①3，6；②点的坐标为(0，1)或(0，-1)；（2）或

【解析】

(1)①由题意得出M=OB=3，m=3，即可得出点O到线段AB的“极化距离”；由题意可得点E、点A、点B三点共线，可得M=AE=8，m=BE=2，即可得点E(-5，3)到线段AB的“极化距离”；

②分两种情况讨论，设点P(0，a)，利用勾股定理可求M，由题意列出方程可求解；
(2)分两种情况讨论，取特殊位置当t=2、t=0、t=时，分别求解即可解决问题．

(1)如图，连接BO，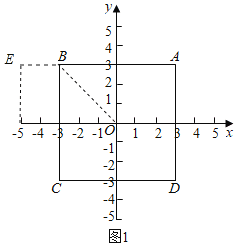

∵正方形ABCD以原点O为中心，点A的坐标为(3，3)，
∴点O(0，0)，B(-3，3)
∴OB=3，
∴M=OB=3，m=3，
∴点O到线段AB的“极化距离”D(O，AB)=3，

∵点E(-5，3)，点A(3，3)，点B(-3，3)
∴点E、点A、点B三点共线，
∴M=AE=8，m=BE=2，
∴点E(-5，3)到线段AB的“极化距离”D(E，AB)=6，
故答案为：3，6；

②如下图记，

若在轴正半轴，有两种情况：

在线段上，则，．

设点P(0，)，

∴M=CP=，m=()，
∵D(P，W)=3，
∴

∴，
∴点P坐标(0，1)，

若在F上方，可知，无解，

由对称性，若在轴正半轴，可得点P(0，-1)；

综上，点P坐标为(0，1)或(0，-1)；

(2)∵直线与轴，轴分别交于F，G两点，

令，则，令，则，
∴点F坐标(-1，0)，点G(0，1)，
当t≥0时，
如图，当t=2时，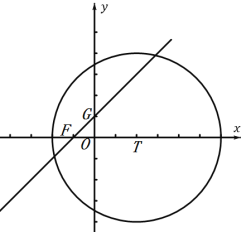

由图可得：M=7，m=1，
∴D(P，W)=6，

如图，当t=0时，

由图可得：M=5，m=3，

∴D(P，W)=2，
∴当0＜t＜2时，线段FG上的任一点P都满足2＜D(P，W)＜6，
当t＜0时，
如图，延长TG交圆T于H，

依题意，，

∴，

∴，即，

解得：，

∴当时，M=7，m=1，
∴D(P，W)=6，

∴当时，线段FG上的任一点P都满足2＜D(P，W)＜6，
综上所述：或．