题目内容
 如图,将?ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,求证:
如图,将?ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,求证:
(1)MN∥BC;
(2)MN=AM.
证明:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵根据折叠可得∠D=∠NMA,
∴∠B=∠NMA,
∴MN∥BC;
(2)∵四边形ABCD是平行四边形,
∴DN∥AM,AD∥BC,
∵MN∥BC,
∴AD∥MN,
∴四边形AMND是平行四边形,
根据折叠可得AM=DA,
∴四边形AMND为菱形,
∴MN=AM.
分析:(1)根据四边形ABCD是平行四边形,可得∠B=∠D,再根据折叠可得∠D=∠NMA,再利用等量代换可得∠B=∠NMA,然后根据平行线的判定方法可得MN∥BC;
(2)首先证明四边形AMND是平行四边形,再根据折叠可得AM=DA,进而可证出四边形AMND为菱形,再根据菱形的性质可得MN=AM.
点评:此题主要考查了翻折变换,以及平行四边形的判定与性质,菱形的判定与性质,关键是找准折叠以后哪些线段是对应相等的,哪些角是对应相等的.
∴∠B=∠D,
∵根据折叠可得∠D=∠NMA,
∴∠B=∠NMA,
∴MN∥BC;
(2)∵四边形ABCD是平行四边形,
∴DN∥AM,AD∥BC,
∵MN∥BC,
∴AD∥MN,
∴四边形AMND是平行四边形,
根据折叠可得AM=DA,
∴四边形AMND为菱形,
∴MN=AM.
分析:(1)根据四边形ABCD是平行四边形,可得∠B=∠D,再根据折叠可得∠D=∠NMA,再利用等量代换可得∠B=∠NMA,然后根据平行线的判定方法可得MN∥BC;
(2)首先证明四边形AMND是平行四边形,再根据折叠可得AM=DA,进而可证出四边形AMND为菱形,再根据菱形的性质可得MN=AM.
点评:此题主要考查了翻折变换,以及平行四边形的判定与性质,菱形的判定与性质,关键是找准折叠以后哪些线段是对应相等的,哪些角是对应相等的.

练习册系列答案
相关题目
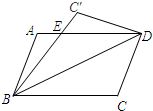 20、如图,将?ABCD沿对角线BD翻折,点C落到点C′处,BC′交AD于点E.
20、如图,将?ABCD沿对角线BD翻折,点C落到点C′处,BC′交AD于点E. 如图,将?ABCD折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,若∠AMF=50°,则∠A等于( )
如图,将?ABCD折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,若∠AMF=50°,则∠A等于( ) 如图,将?ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,求证:
如图,将?ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,求证: 如图,将?ABCD沿对角线BD翻折,点C落到点C′处,BC′交AD于点E.
如图,将?ABCD沿对角线BD翻折,点C落到点C′处,BC′交AD于点E.